《2025年预学与导学八年级数学上册浙教版》

10. 如果一个三角形的三边长$a,b,c满足a^{2}+b^{2}+c^{2}+50 = 6a + 8b + 10c$,那么这个三角形一定是直角三角形。

答案： 直角三角形

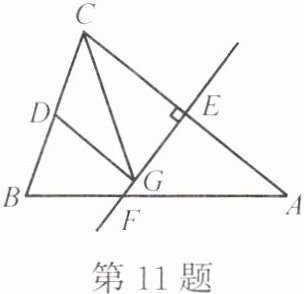
11. 如图,等腰三角形$ABC的底边BC长为4$,面积是$18$,腰$AC的垂直平分线EF分别交边AC,AB于点E,F$。若$D为边BC$的中点,$G为线段EF$上一动点,则$\triangle CDG$周长的最小值为11。

答案： 11

12. 在$\triangle ABC$中,$AB = AC,AB的垂直平分线与AC所在直线相交所得的锐角为42^{\circ}$,则$\angle B = $$66°$或$24°$。

答案： $66°$或$24°$

13. 如图,在$\triangle ABC$中,$CD\perp AB,AB = 2\sqrt{5},BC = 2,AC = 4$。
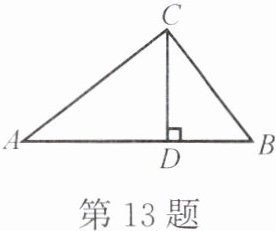
(1) 求证：$\triangle ABC$是直角三角形。
(2) 求$CD$的长。

答案： 1. （1）证明$\triangle ABC$是直角三角形：
解：在$\triangle ABC$中，已知$AB = 2\sqrt{5}$，$BC = 2$，$AC = 4$。
根据勾股定理的逆定理，若$a^{2}+b^{2}=c^{2}$（$c$为最长边），则三角形为直角三角形。
计算$BC^{2}+AC^{2}$的值：
$BC^{2}=2^{2}=4$，$AC^{2}=4^{2}=16$，所以$BC^{2}+AC^{2}=4 + 16=20$。
又因为$AB^{2}=(2\sqrt{5})^{2}=20$。
所以$BC^{2}+AC^{2}=AB^{2}$。
由勾股定理的逆定理可知，$\triangle ABC$是直角三角形，且$\angle C = 90^{\circ}$。
2. （2）求$CD$的长：
解：因为$\triangle ABC$是直角三角形，$CD\perp AB$，根据三角形面积公式$S=\frac{1}{2}ab$（$a,b$为两直角边），也可以表示为$S=\frac{1}{2}ch$（$c$为斜边，$h$为斜边上的高）。
已知$AC = 4$，$BC = 2$，$AB = 2\sqrt{5}$，由$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$。
把$AC = 4$，$BC = 2$，$AB = 2\sqrt{5}$代入$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$中，得到$\frac{1}{2}×4×2=\frac{1}{2}×2\sqrt{5}× CD$。
化简方程：
左边$\frac{1}{2}×4×2 = 4$，右边$\frac{1}{2}×2\sqrt{5}× CD=\sqrt{5}CD$。
则$\sqrt{5}CD = 4$。
解得$CD=\frac{4\sqrt{5}}{5}$。
综上，（1）已证$\triangle ABC$是直角三角形；（2）$CD$的长为$\frac{4\sqrt{5}}{5}$。

14. 在一次数学课上,陈老师在黑板上画出下图,并写下了四个等式：
①$AB = DC$,
②$BE = CE$,
③$\angle B = \angle C$,
④$\angle BAE = \angle CDE$。
要求同学们从这四个等式中选出两个作为条件,推断$\triangle AED$是等腰三角形。
(1) 请你按陈老师的要求写出所有可能的条件：①③；①④；②③；②④。
(2) 任选一种证明。
已知：①③。(填序号)
求证：$\triangle AED$是等腰三角形。
证明：

答案： 1. （1）所有可能的条件：
①③；①④；②③；②④。
2. （2）选①③证明：
已知：①$AB = DC$，③$\angle B=\angle C$。
证明：
在$\triangle ABE$和$\triangle DCE$中，
$\left\{\begin{array}{l}\angle B=\angle C\\\angle AEB = \angle DEC\\AB = DC\end{array}\right.$（$\angle AEB$与$\angle DEC$是对顶角，$\angle AEB=\angle DEC$）。
根据$AAS$（两角及其中一角的对边对应相等的两个三角形全等），可得$\triangle ABE\cong\triangle DCE$。
由全等三角形的性质可知$AE = DE$。
根据等腰三角形的定义（有两边相等的三角形是等腰三角形），所以$\triangle AED$是等腰三角形。
选①④证明：
已知：①$AB = DC$，④$\angle BAE=\angle CDE$。
证明：
在$\triangle ABE$和$\triangle DCE$中，
$\left\{\begin{array}{l}\angle BAE=\angle CDE\\\angle AEB=\angle DEC\\AB = DC\end{array}\right.$（$\angle AEB$与$\angle DEC$是对顶角，$\angle AEB = \angle DEC$）。
根据$AAS$，可得$\triangle ABE\cong\triangle DCE$。
由全等三角形的性质可知$AE = DE$。
所以$\triangle AED$是等腰三角形。
选②③证明：
已知：②$BE = CE$，③$\angle B=\angle C$。
证明：
在$\triangle ABE$和$\triangle DCE$中，
$\left\{\begin{array}{l}\angle B=\angle C\\BE = CE\\\angle AEB=\angle DEC\end{array}\right.$（$\angle AEB$与$\angle DEC$是对顶角，$\angle AEB=\angle DEC$）。
根据$ASA$（两角及其夹边对应相等的两个三角形全等），可得$\triangle ABE\cong\triangle DCE$。
由全等三角形的性质可知$AE = DE$。
所以$\triangle AED$是等腰三角形。
选②④证明：
已知：②$BE = CE$，④$\angle BAE=\angle CDE$。
证明：
在$\triangle ABE$和$\triangle DCE$中，
$\left\{\begin{array}{l}\angle BAE=\angle CDE\\\angle AEB=\angle DEC\\BE = CE\end{array}\right.$（$\angle AEB$与$\angle DEC$是对顶角，$\angle AEB=\angle DEC$）。
根据$AAS$，可得$\triangle ABE\cong\triangle DCE$。
由全等三角形的性质可知$AE = DE$。
所以$\triangle AED$是等腰三角形。

15. 如图,已知$\triangle ABC$。
(1) 请用直尺和圆规在图中作出$\triangle ABC的高线AD以及角平分线AE$。(不写作法,但要保留作图痕迹)
(2) 若$\angle B = 30^{\circ},\angle C = 40^{\circ}$,求$\angle DAE$的度数。

答案： 1. （1）
作高线$AD$：
以$A$为圆心，适当长为半径画弧，交$BC$于两点$M$、$N$；再分别以$M$、$N$为圆心，大于$\frac{1}{2}MN$的长为半径画弧，两弧交于一点$P$，作直线$AP$交$BC$于$D$，则$AD$为$\triangle ABC$的高线。
作角平分线$AE$：
以$A$为圆心，任意长为半径画弧，分别交$AB$、$AC$于$F$、$G$；再分别以$F$、$G$为圆心，大于$\frac{1}{2}FG$的长为半径画弧，两弧交于一点$Q$，作射线$AQ$交$BC$于$E$，则$AE$为$\triangle ABC$的角平分线（作图痕迹略）。
2. （2）
解：
在$\triangle ABC$中，根据三角形内角和定理$\angle A+\angle B+\angle C = 180^{\circ}$。
已知$\angle B = 30^{\circ}$，$\angle C = 40^{\circ}$，则$\angle BAC=180^{\circ}-\angle B - \angle C=180^{\circ}-30^{\circ}-40^{\circ}=110^{\circ}$。
因为$AE$平分$\angle BAC$，所以$\angle BAE=\frac{1}{2}\angle BAC$，即$\angle BAE = \frac{1}{2}×110^{\circ}=55^{\circ}$。
在$Rt\triangle ABD$中，$\angle BAD = 90^{\circ}-\angle B$（直角三角形两锐角互余）。
因为$\angle B = 30^{\circ}$，所以$\angle BAD=90^{\circ}-30^{\circ}=60^{\circ}$。
那么$\angle DAE=\angle BAD-\angle BAE$。
把$\angle BAD = 60^{\circ}$，$\angle BAE = 55^{\circ}$代入可得$\angle DAE=60^{\circ}-55^{\circ}=5^{\circ}$。
综上，$\angle DAE$的度数为$5^{\circ}$。