《2025年中学生世界六年级数学上册沪教版五四制》

14. 已知$|x - 13|= 10$,求$x$.

答案： 解析：本题可根据绝对值的定义来求解$x$的值。
绝对值的定义为：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；$0$的绝对值是$0$。
已知$\vert x - 13\vert = 10$，根据绝对值的定义可知$x - 13$的值为$10$或者$-10$，由此可列出两个方程，分别求解这两个方程即可得到$x$的值。
答案：
解：因为$\vert x - 13\vert = 10$，所以$x - 13 = 10$或$x - 13 = -10$。
当$x - 13 = 10$时，$x = 10 + 13 = 23$；
当$x - 13 = -10$时，$x = -10 + 13 = 3$。
综上，$x$的值为$23$或$3$。

15. 若$|x - 2|+|y + 3|+|z - 5|= 0$,计算：
(1)$x$,$y$,$z$的值；
(2)$|x|+|y|+|z|$的值.

答案：
(1)我们可以按照以下步骤来求$x$，$y$，$z$的值：
由题目信息，可知$|x - 2|+|y + 3|+|z - 5|= 0$。
根据绝对值的性质，绝对值总是大于等于0，即$|a| \geq 0$。
所以，$|x - 2| \geq 0$，$|y + 3| \geq 0$，$|z - 5| \geq 0$。
由于$|x - 2|+|y + 3|+|z - 5|= 0$，且每一项都大于等于0，所以每一项都必须等于0。
即$x - 2 = 0$，$y + 3 = 0$，$z - 5 = 0$。
解这三个方程，得到$x = 2$，$y = -3$，$z = 5$。
(2)我们可以按照以下步骤来求$|x|+|y|+|z|$的值：
由第一问已知$x = 2$，$y = -3$，$z = 5$。
根据绝对值的定义，正数的绝对值是其本身，负数的绝对值是它的相反数。
所以，$|x| = 2$，$|y| = 3$，$|z| = 5$。
将这三个值相加，得到$|x|+|y|+|z| = 2 + 3 + 5 = 10$。

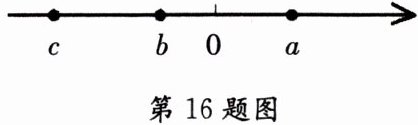
16. 设三个有理数$a$,$b$,$c$在数轴上对应点如图所示.化简：

(1)$|b - a|$；
(2)$|a + c|$；
(3)$|c - b|$.

答案： 解析：本题可根据绝对值的性质以及数轴上数的大小关系来化简绝对值。
在数轴上，右边的数总比左边的数大，由图可知$c\lt b\lt0\lt a$，且$\vert c\vert\gt\vert a\vert\gt\vert b\vert$。
（1）化简$\vert b - a\vert$：
因为$b\lt a$，所以$b - a\lt0$。
根据绝对值的性质：当$x\lt0$时，$\vert x\vert=-x$，可得$\vert b - a\vert=-(b - a)=a - b$。
（2）化简$\vert a + c\vert$：
因为$c\lt0$，$a\gt0$，且$\vert c\vert\gt\vert a\vert$，即$-c\gt a$，所以$a + c\lt0$。
根据绝对值的性质：当$x\lt0$时，$\vert x\vert=-x$，可得$\vert a + c\vert=-(a + c)=-a - c$。
（3）化简$\vert c - b\vert$：
因为$c\lt b$，所以$c - b\lt0$。
根据绝对值的性质：当$x\lt0$时，$\vert x\vert=-x$，可得$\vert c - b\vert=-(c - b)=b - c$。
答案：
(1)$a - b$；
(2)$-a - c$；
(3)$b - c$。