《2025年中学生世界六年级数学上册沪教版五四制》

12. 某地气象站测得某天的四个时刻气温分别为:早晨 6 时为零下 $3^{\circ}C$,中午 12 时为零上 $1^{\circ}C$,下午 4 时为 $0^{\circ}C$,晚上 12 时为零下 $9^{\circ}C$.请用正数、负数或零表示这四个不同时刻的温度.

答案： 分析：
这道题目考查了正数、负数和零在实际问题中的应用。
题目给出了四个不同时刻的气温，其中涉及零上温度、零下温度和零度。
我们需要根据这些描述，用正数、负数或零来表示这些温度。
早晨6时气温为零下$3^{\circ}C$，表示为$-3^{\circ}C$。
中午12时气温为零上$1^{\circ}C$，表示为$+1^{\circ}C$或简化为$1^{\circ}C$。
下午4时气温为$0^{\circ}C$，表示为$0$。
晚上12时气温为零下$9^{\circ}C$，表示为$-9^{\circ}C$。
答案：
早晨6时：$-3^{\circ}C$
中午12时：$1^{\circ}C$
下午4时：$0^{\circ}C$
晚上12时：$-9^{\circ}C$

13. 学校对六年级男生进行立定跳远测试,以能跳 1.6 m 及以上为达标,超过 1.6 m 的部分用正数表示,不足 1.6 m 的部分用负数表示.
某组 10 名男生的立定跳远成绩如下表(单位:cm):
|1|2|3|4|5|6|7|8|9|10|
|+2|-4|0|+5|+8|-7|0|+2|+10|-3|
问:(1)这一组有几位同学达标?
(2)这一组第几号同学立定跳远成绩最好? 是多远?

答案：
(1) 解：达标的成绩为非负数，表中成绩为+2、0、+5、+8、0、+2、+10的同学达标，共7位。
(2) 解：成绩最好即超过1.6m最多，+10最大，对应9号同学，成绩为1.6m + 10cm = 1.7m。
(1) 7位；
(2) 9号，1.7m。

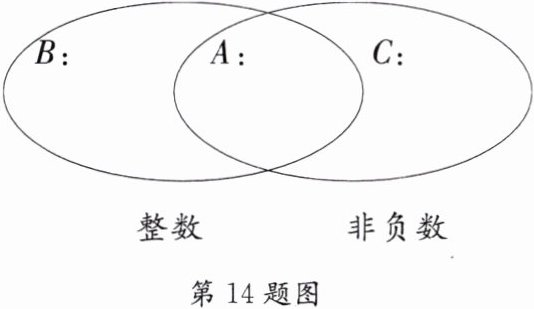
14. 如右图,两个圈分别表示整数和非负数.
(1)在图中画线处各填入符合条件的三个有理数;
(2)你能说出 $A,B,C$ 三部分分别表示的是什么数吗?

答案：
(1) B: -1, -2, -3；A: 0, 1, 2；C: 0.5, 1.2, 3.6。
(2) A：非负整数；B：负整数；C：正分数。

观察一组顺次排列的有理数: $-2,\frac{3}{2},-\frac{4}{3},\frac{5}{4},-\frac{6}{5},…$ 你能说出这组数排列的规律吗? 根据这个规律,第 2021 个数是什么?

答案： 解析：
首先，我们观察这组数的符号，发现它们是交替出现的，即第1个数是负数，第2个数是正数，第3个数是负数，以此类推。因此，我们可以推断出第$n$个数的符号是$(-1)^n$。
其次，我们观察这组数的绝对值部分。第1个数的绝对值是2，可以表示为$\frac{2}{1}$；第2个数的绝对值是$\frac{3}{2}$；第3个数的绝对值是$\frac{4}{3}$；以此类推。我们可以发现，第$n$个数的绝对值部分可以表示为$\frac{n+1}{n}$。
综合以上两点，我们可以得出这组数的通项公式为：第$n$个数 = $(-1)^n × \frac{n+1}{n}$。
根据这个公式，我们可以求出第2021个数：
答案：
第2021个数 = $(-1)^{2021} × \frac{2021+1}{2021} = -\frac{2022}{2021}$。