《2025年中学生世界六年级数学上册沪教版五四制》

1. 计算 $4(a + 2)-2a$ 等于(C)
A.$2a + 2$；
B.$2a - 2$；
C.$2a + 8$；
D.$2a - 8$.

答案： 解：$4(a + 2)-2a$
$=4a + 8 - 2a$
$=2a + 8$
答案：C

2. 数与一次式相乘,依据的运算律是(D)
A.加法结合律；
B.乘法交换律；
C.乘法结合律；
D.乘法分配律.

答案： D

3. 下列计算正确的是(D)
A.$-3(5y - 9)= -15y - 9$；
B.$-3(5y - 9)= -15y + 9$；
C.$-(-y - 9)= y - 9$；
D.$-(-y - 9)= y + 9$.

答案： 解：
A. $-3(5y - 9) = -15y + 27$，故A错误；
B. $-3(5y - 9) = -15y + 27$，故B错误；
C. $-(-y - 9) = y + 9$，故C错误；
D. $-(-y - 9) = y + 9$，故D正确。
答案：D

4. 某城市出租车的收费标准是：起步价 13 元,当路程超过 $3\mathrm{km}$ 时,每千米收费 2 元. 如果某出租车载客行驶了 $x(x＞3$ 千米),那么出租车司机应收费多少元？(A)
A.$13 + 2(x - 3)$；
B.$13 + 2x$；
C.$13 - 2x - 3$；
D.$13 - 2(x - 3)$.

答案： 解：因为出租车行驶路程$x＞3$千米，所以收费分为两部分：起步价13元与超过3千米的费用。超过3千米的路程为$(x - 3)$千米，每千米收费2元，超过部分费用为$2(x - 3)$元。总收费为起步价加上超过部分费用，即$13 + 2(x - 3)$元。
答案：A

5. 计算：$5(3x + 5y - 1)= $$15x + 25y - 5$.

答案： 解析：本题可根据乘法分配律来计算。乘法分配律是指两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再相加。用字母表示为$a(b + c)=ab + ac$。
对于$5(3x + 5y - 1)$，将$5$分别与括号内的每一项相乘，即：
$5×3x+5×5y - 5×1$
$=15x + 25y - 5$
答案：$15x + 25y - 5$

6. 计算：$-4(x - y + 3)= $$-4x + 4y - 12$.

答案： 解：$-4(x - y + 3)$
$= -4 \cdot x + (-4) \cdot (-y) + (-4) \cdot 3$
$= -4x + 4y - 12$
$-4x + 4y - 12$

7. 已知 $x - y = 3$,那么 $-3x + 3y - 1$ 的值是-10.

答案： 解：因为 $x - y = 3$，所以 $-3x + 3y = -3(x - y) = -3×3 = -9$，则 $-3x + 3y - 1 = -9 - 1 = -10$。
$-10$

8. 如果一次式 $3x - 1$ 与 $-4x + 6$ 的值互为相反数,那么 $x$ 的值是5.

答案： 解：因为一次式$3x - 1$与$-4x + 6$的值互为相反数，所以$(3x - 1) + (-4x + 6) = 0$
$3x - 1 - 4x + 6 = 0$
$-x + 5 = 0$
$-x = -5$
$x = 5$
5

9. 如果两个一次式的和是 0,那么这两个一次式可以是$x$ 和 $-x$(只需写出一组即可).

答案： 解析：两个一次式的和为0，即这两个一次式互为相反数。
答案：$x$ 和 $-x$（答案不唯一）。

10. $A$ 为一次式,如果 $-4(3m - 4n + 2)-A = m + n - 8$,那么 $A=$$-13m + 15n$.

答案： 解析：
本题主要考查一次式的运算。
根据题目条件，有等式 $-4(3m - 4n + 2)-A = m + n - 8$。
首先，去括号，得到 $-12m + 16n - 8 - A = m + n - 8$。
接着，将等式两边的常数项和同类项进行合并，以便解出 $A$。
即：$-12m + 16n - m - n = A - 8 + 8$，
化简得：$-13m + 15n = A$。
答案：$-13m + 15n$。

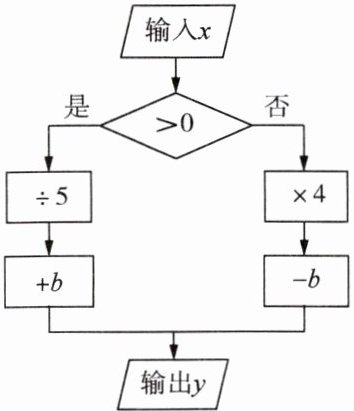
11. 程序图的算法源于我国数学名著《九章算术》,如图所示的程序图,当输入 $x$ 的值为 15 时,输出 $y$ 的值是 4；若当输入 $x$ 的值为 $-\frac{1}{4}$ 时,则输出 $y$ 的值为-2.

答案： 解：由程序图可知，当$x＞0$时，$y = \frac{x}{5} + b$；当$x\leqslant0$时，$y = 4x - b$。
当$x = 15$时，$15＞0$，则$y=\frac{15}{5}+b=3 + b$。已知此时$y = 4$，可得$3 + b=4$，解得$b = 1$。
当$x=-\frac{1}{4}$时，$-\frac{1}{4}＜0$，则$y=4×(-\frac{1}{4})-1=-1 - 1=-2$。
$-2$

12. 计算：(1) $3 - 4(2x - 3y - 1)$；(2) $-\frac{1}{2}(4m - 2)-\frac{1}{3}(6 - 12m)$.

答案： 解析：
(1) 本题考查了数与一次式相乘的运算法则。需要先将括号内的每一项分别与括号外的数相乘，再合并同类项。
(2) 本题同样考查了数与一次式相乘的运算法则，并且涉及到分数的运算。需要先将括号内的每一项分别与括号外的分数相乘，注意分数的运算规则，再合并同类项。
答案：
(1) $3 - 4(2x - 3y - 1)$
$= 3 - 8x + 12y + 4$
$= 7 - 8x + 12y$
(2) $-\frac{1}{2}(4m - 2)-\frac{1}{3}(6 - 12m)$
$= -2m + 1 - 2 + 4m$
$= 2m - 1$