《2025年中学生世界六年级数学上册沪教版五四制》

11. 在下图中,用数轴上的点分别表示3.5,$\frac{1}{3},$$-2\frac{1}{4},$0.

答案：

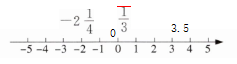
12. 在数轴上,点A和点B分别表示-3和2,应怎样移动点A,才能使点A表示的数是点B表示的数的5倍?

答案： 解析：
本题主要考察数轴上的点与有理数的关系，以及有理数的运算。
首先，我们需要找出点B表示的数的5倍，即$2 × 5 = 10$。
然后，我们需要考虑如何将点A从-3移动到10。
在数轴上，一个点向右移动相当于对该点表示的数进行加法运算，向左移动相当于进行减法运算。
因此，我们需要计算点A需要向右移动多少单位才能从-3变为10。
这个移动单位可以通过计算$10 - (-3)$得出。
答案：
点A需要向右移动13个单位，才能使点A表示的数是点B表示的数的5倍。

13. 六(4)班在一次联欢活动中,把全班学生分成五个队参加游戏.游戏结束后,五个队的得分情况是：A队：-50分；B队：150分；C队：-200分；D队：0分；E队：100分.
(1)将五个队的分数按由低分到高分的顺序排序；
(2)把每个队的得分标在数轴上,并将代表该队的字母标上；
(3)从数轴上看,A队与B队相差多少分? C队与E队呢?

答案： 解析：
本题主要考查有理数的大小比较和数轴上的表示，以及有理数的减法运算。
(1) 根据有理数的大小比较规则，正数大于0，0大于负数，正数大于一切负数，两个负数绝对值大的反而小，所以可以将五个队的分数按由低分到高分的顺序排序。
(2) 在数轴上，正数位于0的右侧，负数位于0的左侧，绝对值表示该数到0的距离。因此，可以根据每个队的得分，在数轴上找到对应的位置，并标上代表该队的字母。
(3) 在数轴上，两点间的距离等于它们坐标之差的绝对值。所以，A队与B队的分数差等于B队的分数减去A队的分数，C队与E队的分数差等于E队的分数减去C队的分数。
答案：
(1) 五个队的分数按由低分到高分的顺序排序为：C队（-200分），A队（-50分），D队（0分），E队（100分），B队（150分）。
(2) 数轴上的表示略（图略）。在数轴上，-200对应C队，-50对应A队，0对应D队，100对应E队，150对应B队。
(3) A队与B队相差的分数为：$150 - (-50) = 200$分；C队与E队相差的分数为：$100 - (-200) = 300$分。

如图,数轴上相邻刻度的距离表示单位长度,点A、B、C、D所表示的数均为整数.若点A表示数a,点B表示数b,且b - 2a = 7.你能在数轴上找出原点的位置吗?

答案： 解析：本题考查数轴上点的表示以及代数式的运用。
设点$A$表示的数为$a$，因为点$B$在点$A$右侧相隔$3$个单位长度，所以点$B$表示的数$b = a + 3$。
已知$b - 2a = 7$，将$b = a + 3$代入$b - 2a = 7$中，得到$(a + 3) - 2a = 7$。
对$(a + 3) - 2a = 7$进行化简求解：
$\begin{aligned}a + 3 - 2a&= 7\\3 - a&= 7\\-a&= 7 - 3\\-a&= 4\\a&= -4\end{aligned}$
因为点$A$表示的数$a = -4$，从点$A$向右移动$4$个单位长度就是原点，此时原点刚好在点$B$左侧相隔$1$个单位长度处。
答案：在数轴上，点$A$表示的数为$-4$，从点$A$向右移动$4$个单位长度可找到原点，原点在点$B$左侧相隔$1$个单位长度处。