《2025年中学生世界六年级数学上册沪教版五四制》

1. 下列代数式是一次式的是(C)
A.$a^{2}+1$；
B.$-5$；
C.$2a + 2b$；
D.$\frac{1}{a}$。

答案： 解析：本题可根据一次式的定义来逐一分析选项。一次式是数与字母的积或字母与字母的积所组成的代数式，单独的一个数或一个字母也叫做一次式，且一次式中字母的指数都为$1$。
选项 A：$a^{2}+1$中$a$的指数是$2$，不是一次式。
选项 B：$-5$是单独的一个数，虽然它是一次式，但本题更侧重于含字母的一次式判断，相比之下该选项不是最符合题意的典型一次式形式。
选项 C：$2a + 2b$是数$2$与字母$a$、$2$与字母$b$的积的和，字母$a$和$b$的指数都为$1$，符合一次式的定义。
选项 D：$\frac{1}{a}$分母中含有字母，它是分式，不是整式，更不是一次式。
答案：C。

2. 下列关于代数式“$-m + 2n - 4$”说法正确的是(D)
A.它的一次项是 $2n$；
B.它的一次项系数是 $2$；
C.它的常数项是 $4$；
D.它表示 $-m$,$2n$,$-4$ 的和。

答案： 解：
A. 一次项是$-m$和$2n$，故A错误；
B. 一次项系数是$-1$和$2$，故B错误；
C. 常数项是$-4$，故C错误；
D. 它表示$-m$，$2n$，$-4$的和，故D正确。
答案：D

3. 当 $x = -2$ 时,一次式 $8 - 3x$ 的值是(B)
A.$2$；
B.$14$；
C.$3$；
D.$7$。

答案： 解：当$x = -2$时，
$8 - 3x = 8 - 3×(-2)$
$= 8 + 6$
$= 14$
答案：B

4. 如果一个两位数的个位上的数是 $a$,十位上的数是 $b$,那么这个两位数是(D)
A.$ab$；
B.$b + a$；
C.$10a + b$；
D.$10b + a$。

答案： 解：两位数中，十位上的数字表示几个十，个位上的数字表示几个一。已知十位上的数是$b$，则表示$b$个十，即$10b$；个位上的数是$a$，则表示$a$个一，即$a$。所以这个两位数是$10b + a$。
答案：D

5. 当 $x = 1$,$y = -2$ 时,一次式 $2x + y$ 的值是0。

答案： 解：当$x = 1$，$y = -2$时，
$2x + y = 2×1 + (-2)$
$= 2 - 2$
$= 0$
0

6. 如果一次式 $\frac{x - 3}{4}$ 的值为 $1$,那么 $x$ 的值为7。

答案： 解析：本题可根据已知条件列出方程，再通过解方程求出$x$的值。
已知一次式$\frac{x - 3}{4}$的值为$1$，可列出方程$\frac{x - 3}{4}=1$。
根据等式的性质，等式两边同时乘以$4$，得到$\frac{x - 3}{4}×4 = 1×4$，即$x - 3 = 4$。
等式两边再同时加上$3$，得到$x - 3 + 3 = 4 + 3$，解得$x = 7$。
答案：$7$。

7. 已知 $3x - 7y = -2$,则 $9x - 21y + 8$ 的值是______2。

答案： 解：因为 $3x - 7y = -2$，所以 $9x - 21y = 3(3x - 7y) = 3×(-2) = -6$。则 $9x - 21y + 8 = -6 + 8 = 2$。
2

8. 已知 $|3x - 1| + |2y + 3| = 0$,则一次式 $3x - 2y$ 的值是4。

答案： 解：因为$|3x - 1| + |2y + 3| = 0$，且绝对值具有非负性，所以$|3x - 1| = 0$，$|2y + 3| = 0$。
由$|3x - 1| = 0$，得$3x - 1 = 0$，解得$x = \frac{1}{3}$。
由$|2y + 3| = 0$，得$2y + 3 = 0$，解得$y = -\frac{3}{2}$。
将$x = \frac{1}{3}$，$y = -\frac{3}{2}$代入$3x - 2y$，得：
$3×\frac{1}{3} - 2×(-\frac{3}{2}) = 1 + 3 = 4$。
故答案为：4。

9. 一次式 $-3m + \frac{3}{5}n - 4$ 中的一次项是$-3m$，$\frac{3}{5}n$,常数项是$-4$。

答案： 解：一次项是$-3m$，$\frac{3}{5}n$；常数项是$-4$。

10. 如果一个正方形的周长为 $a$,那么它的边长是$\frac{a}{4}$（或 $0.25a$）,面积是$\frac{a^2}{16}$。

答案： 解析：
本题主要考查正方形的周长和面积公式以及代数式的表示。
正方形的周长公式为：$P = 4s$，其中$P$是周长，$s$是边长。
根据题意，正方形的周长为$a$，所以：
$4s = a$。
从上式，我们可以解出边长$s$为：
$s = \frac{a}{4}$，即$\frac{a}{4}$也可以写成$0.25a$。
正方形的面积公式为：$S = s^2$，其中$S$是面积，$s$是边长。
将边长$s = \frac{a}{4}$代入面积公式，得到：
$S =(\frac{a}{4})^2 = \frac{a^2}{16}$。
答案：
边长是：$\frac{a}{4}$（或 $0.25a$）；
面积是：$\frac{a^2}{16}$。

11. 如果三个连续奇数中,中间的一个数为 $2n + 1$,用一次式表示这三个连续奇数的和是$6n + 3$。当 $n = 2$ 时,这个一次式的和是$15$。

答案： 解：因为三个连续奇数中，中间的一个数为$2n + 1$，所以前一个奇数为$2n + 1 - 2 = 2n - 1$，后一个奇数为$2n + 1 + 2 = 2n + 3$。
这三个连续奇数的和为：$(2n - 1) + (2n + 1) + (2n + 3)$
$=2n - 1 + 2n + 1 + 2n + 3$
$=(2n + 2n + 2n) + (-1 + 1 + 3)$
$=6n + 3$
当$n = 2$时，$6n + 3 = 6×2 + 3 = 15$
$6n + 3$；$15$

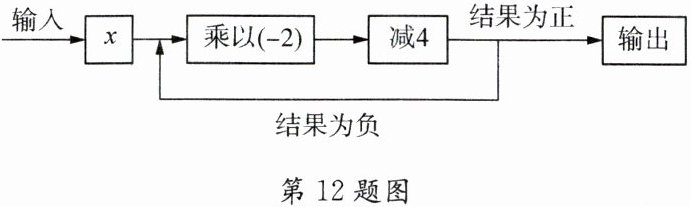
12. 按下列程序输入一个数 $x$,若输入的数 $x = 0$,则输出的结果为4。

答案： 当$x = 0$时，
第一次计算：$0×(-2)-4=-4$，结果为负；
第二次计算：$(-4)×(-2)-4=8 - 4 = 4$，结果为正。
所以输出的结果为$4$。
答案：$4$。

13. $S$ 为梯形的面积,$a$,$b$ 分别为梯形的上底和下底边长,$h$ 为梯形的高。
(1)写出梯形的面积公式是：$S=\frac{(a+b)h}{2}$；
(2)当 $S = 24$,$a = 3$,$b = 9$ 时,求梯形的高 $h$；
解：将$S = 24$，$a = 3$，$b = 9$代入$S=\frac{(a+b)h}{2}$，得$24=\frac{(3 + 9)h}{2}$，$24=\frac{12h}{2}$，$24 = 6h$，$h=4$
(3)当 $a = 1$,$b = 4$,$h = 3$ 时,求梯形的面积 $S$。
解：将$a = 1$，$b = 4$，$h = 3$代入$S=\frac{(a+b)h}{2}$，得$S=\frac{(1 + 4)×3}{2}=\frac{5×3}{2}=\frac{15}{2}=7.5$

答案：
(1)$S=\frac{(a+b)h}{2}$
(2)解：将$S = 24$，$a = 3$，$b = 9$代入$S=\frac{(a+b)h}{2}$，得$24=\frac{(3 + 9)h}{2}$，$24=\frac{12h}{2}$，$24 = 6h$，$h=4$
(3)解：将$a = 1$，$b = 4$，$h = 3$代入$S=\frac{(a+b)h}{2}$，得$S=\frac{(1 + 4)×3}{2}=\frac{5×3}{2}=\frac{15}{2}=7.5$