《2025年假期面对面南方出版社八年级数学沪科版》

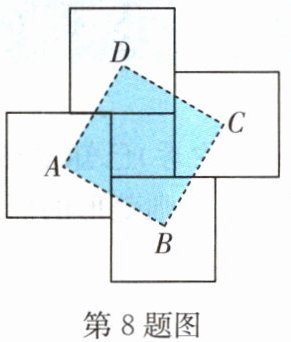
8.(台州中考)用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖面积为a，小正方形地砖面积为b.依次连接四块大正方形地砖的中心得到正方形ABCD，则正方形ABCD的面积为a + b(用含a，b的代数式表示).

答案： $ a + b $

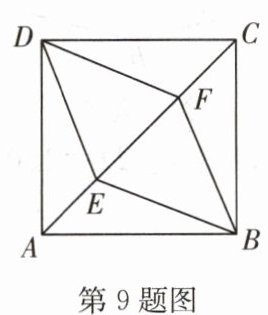
9.(枣庄中考)如图，E，F是正方形ABCD的对角线AC上的两点，AC=8，AE=CF=2，则四边形BEDF的周长是$8\sqrt{5}$.

答案： $ 8 \sqrt { 5 } $

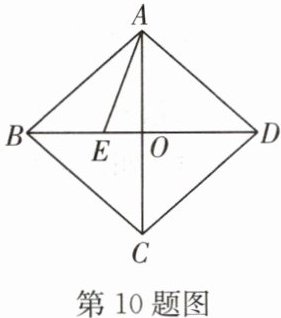
10.(哈尔滨中考)如图，在菱形ABCD中，对角线AC，BD相交于点O，点E在线段BO上，连接AE，若CD=2BE，∠DAE=∠DEA，EO=1，则线段AE的长为$ 2 \sqrt { 2 } $.

答案： $ 2 \sqrt { 2 } $

11.(江西中考)如图，四边形ABCD中，AB=CD，AD=BC，对角线AC，BD相交于点O，且OA=OD.
求证：四边形ABCD是矩形.
证明：∵AB=CD，AD=BC，∴四边形ABCD是平行四边形，∴OA=1/2AC，OD=1/2BD。又∵OA=OD，∴AC=BD，∴四边形ABCD是矩形。

答案： 证明：$\because AB = CD$，$AD = BC$，$\therefore$ 四边形 $ABCD$ 是平行四边形，$\therefore OA = \frac { 1 } { 2 } AC$，$OD = \frac { 1 } { 2 } BD$。又 $\because OA = OD$，$\therefore AC = BD$，$\therefore$ 四边形 $ABCD$ 是矩形。

12.(内江中考)如图，在正方形ABCD中，点E是BC上的一点，点F是CD延长线上的一点，且BE=DF，连接AE，AF，EF.
(1)求证：△ABE≌△ADF；
证明：$\because$ 四边形 $ABCD$ 是正方形，$\therefore AB = AD$，$\angle B = \angle ADC = 90 ^ { \circ }$，$\therefore \angle B = \angle ADF = 90 ^ { \circ }$。又 $\because BE = DF$，$\therefore \triangle ABE \cong \triangle ADF$SAS。
(2)若AE=5，请求出EF的长.
解：$\because \triangle ABE \cong \triangle ADF$，$\therefore AF = AE = 5$，$\angle FAD = \angle BAE$，$\therefore \angle FAE = \angle BAD = 90 ^ { \circ }$。在 $Rt \triangle AEF$ 中，由勾股定理得，$EF =\sqrt { A E ^ { 2 } + A F ^ { 2 } } = \sqrt { 5 ^ { 2 } + 5 ^ { 2 } } =$$5\sqrt{2}$。

答案：
(1) 证明：$\because$ 四边形 $ABCD$ 是正方形，$\therefore AB = AD$，$\angle B = \angle ADC = 90 ^ { \circ }$，$\therefore \angle B = \angle ADF = 90 ^ { \circ }$。又 $\because BE = DF$，$\therefore \triangle ABE \cong \triangle ADF ( SAS )$。
(2) 解：$\because \triangle ABE \cong \triangle ADF$，$\therefore AF = AE = 5$，$\angle FAD = \angle BAE$，$\therefore \angle FAE = \angle BAD = 90 ^ { \circ }$。在 $Rt \triangle AEF$ 中，由勾股定理得，$EF =\sqrt { A E ^ { 2 } + A F ^ { 2 } } = \sqrt { 5 ^ { 2 } + 5 ^ { 2 } } = 5 \sqrt { 2 }$。

13.(德阳中考)如图，四边形ABCD为矩形，G是对角线BD的中点，连接GC并延长至F，使CF=GC，以DC，CF为邻边作菱形DCFE，连接CE.
(1)判断四边形CEDG的形状，并证明你的结论；
四边形CEDG的形状是菱形
(2)连接DF，若BC=$\sqrt{3}$，求DF的长.
DF的长为$\sqrt{3}$

答案： 解：
(1) 四边形 $CEDG$ 是菱形。证明：$\because$ 四边形 $DCFE$ 是菱形，$\therefore DE // GF$，$CF = EF = DE = CD$。$\because CF = GC$，$\therefore DE = GC$，$\therefore$ 四边形 $CEDG$ 是平行四边形。$\because \angle BCD = 90 ^ { \circ }$，点 $G$ 是 $BD$ 的中点，$\therefore CG = BG = DG$，$\therefore$ 四边形 $CEDG$ 是菱形。
(2) $\because CG = DG = DE = CD = CF = EF = CE$，$\therefore \triangle CGD$，$\triangle CDE$，$\triangle CEF$ 都是等边三角形，$\therefore \angle CDG = \angle DGC = \angle CDE = 60 ^ { \circ }$，$\therefore CD = \frac { 1 } { 2 } BD$。又 $\because$ 四边形 $DCFE$ 是菱形，$\therefore \angle CDF = \frac { 1 } { 2 } \angle CDE = 30 ^ { \circ }$，$\therefore \angle GDF = \angle CDG + \angle CDF = 90 ^ { \circ }$。$\because BC = \sqrt { 3 }$，$BC ^ { 2 } + CD ^ { 2 } = BD ^ { 2 }$，$\therefore CD = 1$，$\therefore DG = 1$，$\because GF = 2$，$\therefore DF = \sqrt { G F ^ { 2 } - D G ^ { 2 } } = \sqrt { 3 }$。