2025年假期面对面南方出版社八年级数学沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期面对面南方出版社八年级数学沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1.(南通中考)下列长度的三条线段能组成直角三角形的是(
A.3,4,5
B.2,3,4
C.4,6,7
D.5,11,12
A
)A.3,4,5
B.2,3,4
C.4,6,7
D.5,11,12
答案:
A
2.(泸州中考)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为(

A.9
B.6
C.4
D.3
D
)
A.9
B.6
C.4
D.3
答案:
D
3.(河北中考)如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按如图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是(

A.1,4,5
B.2,3,5
C.3,4,5
D.2,2,4
B
)
A.1,4,5
B.2,3,5
C.3,4,5
D.2,2,4
答案:
B
4.(德阳中考)《九章算术》是我国古代一部著名的数学专著,其中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?其意思是:有一根与地面垂直且高一丈的竹子(1丈=10尺),现被大风折断成两截,尖端落在地面上,竹尖与竹根的距离为三尺.问折断处离地面的距离为(
A.5.45尺
B.4.55尺
C.5.8尺
D.4.2尺
B
)A.5.45尺
B.4.55尺
C.5.8尺
D.4.2尺
答案:
B
5.(益阳中考)已知M,N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是(
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
B
)A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
答案:
B
6.(陕西中考)如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为(
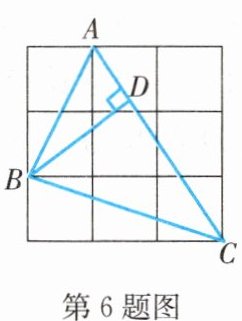
A.$\frac {10}{13}\sqrt {13}$
B.$\frac {9}{13}\sqrt {13}$
C.$\frac {8}{13}\sqrt {13}$
D.$\frac {7}{13}\sqrt {13}$
D
)
A.$\frac {10}{13}\sqrt {13}$
B.$\frac {9}{13}\sqrt {13}$
C.$\frac {8}{13}\sqrt {13}$
D.$\frac {7}{13}\sqrt {13}$
答案:
D
7.(宁波中考)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出(
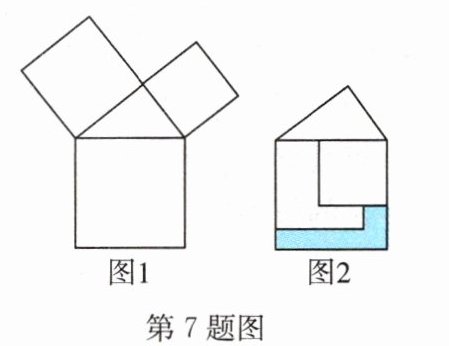
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
C
)
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
答案:
C
8.(枣庄中考)如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为(
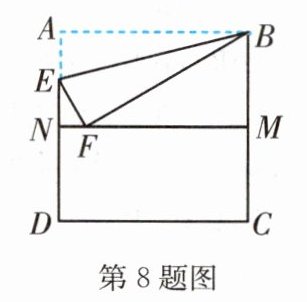
A.2
B.$\sqrt {3}$
C.$\sqrt {2}$
D.1
B
)
A.2
B.$\sqrt {3}$
C.$\sqrt {2}$
D.1
答案:
B
9.(东营中考)如图,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是(
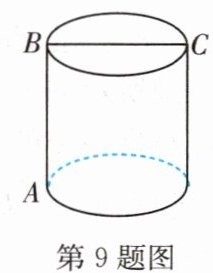
A.$3\sqrt {1+π}$
B.$3\sqrt {2}$
C.$\frac {3\sqrt {4+π^{2}}}{2}$
D.$3\sqrt {1+π^{2}}$
C
)
A.$3\sqrt {1+π}$
B.$3\sqrt {2}$
C.$\frac {3\sqrt {4+π^{2}}}{2}$
D.$3\sqrt {1+π^{2}}$
答案:
C
查看更多完整答案,请扫码查看


