《2025年假期面对面南方出版社八年级数学沪科版》

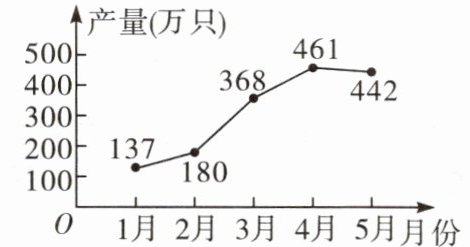
某厂家2024年1~5月份的口罩产量统计如图所示。设从2月份到4月份，该厂家口罩产量的平均月增长率为x，根据题意可得方程（B）
2024年1~5月份某厂家的口罩产量统计图

A. $ 180(1 - x)^2 = 461 $
B. $ 180(1 + x)^2 = 461 $
C. $ 368(1 - x)^2 = 442 $
D. $ 368(1 + x)^2 = 442 $

答案： 【分析】根据折线统计图可知，2月份的口罩产量是180万只，4月份的口罩产量是461万只，故可得方程$ 180(1 + x)^2 = 461 $。故选B。
【解答】B
【点拨】本题考查了由实际问题抽象出一元二次方程，考的是增长率问题，一般形式为$ a(1 + x)^2 = b $，a为起始时间的有关数量，b为终止时间的有关数量。

1.（河南中考）国家统计局统计数据显示，我国快递业务收入逐年增加。2021年至2023年我国快递业务收入由10 332亿元增加到10 634亿元。设我国2021年至2023年快递业务收入的年平均增长率为x，则可列方程为（C）
A. $ 10 332(1 + 2x) = 10 634 $
B. $ 10 332×2(1 + x) = 10 634 $
C. $ 10 332(1 + x)^2 = 10 634 $
D. $ 10 332 + 10 332(1 + x) + 10 332(1 + x)^2 = 10 634 $

答案： C

2. 疫情期间，某快递公司推出无接触配送服务，第1周接到5万件订单，第2周到第3周订单量增长率是第1周到第2周订单量增长率的1.5倍，若第3周接到订单为7.8万件，设第1周到第2周的订单增长率为x，可列得方程为（D）
A. $ 5(1 + x + 1.5x) = 7.8 $
B. $ 5(1 + x×1.5x) = 7.8 $
C. $ 7.8(1 - x)(1 - 1.5x) = 5 $
D. $ 5(1 + x)(1 + 1.5x) = 7.8 $

答案： D

3. 有x支球队参加篮球比赛，共比赛了45场，每两队之间都比赛一场，则下列方程中符合题意的是（A）
A. $ \frac{1}{2}x(x - 1) = 45 $
B. $ \frac{1}{2}x(x + 1) = 45 $
C. $ x(x - 1) = 45 $
D. $ x(x + 1) = 45 $

答案： A

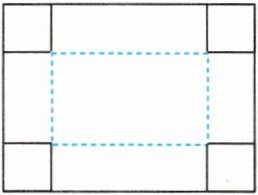
4.（遵义中考）如图，把一块长为40 cm，宽为30 cm的矩形硬纸板的四角剪去四个相同的小正方形，然后把纸板的四边沿虚线折起，并用胶带粘好，即可做成一个无盖纸盒。若该无盖纸盒的底面积为$ 600 cm^2 $，设剪去小正方形的边长为x cm，则可列方程为（D）

A. $ (30 - 2x)(40 - x) = 600 $
B. $ (30 - x)(40 - x) = 600 $
C. $ (30 - x)(40 - 2x) = 600 $
D. $ (30 - 2x)(40 - 2x) = 600 $

答案： D

5. 某校进行体操队列训练，原有8行10列，后增加40人，使得队伍增加的行数、列数相同，你知道增加了多少行或多少列吗？设增加了x行或列，则列方程得（D）
A. $ (8 - x)(10 - x) = 8×10 - 40 $
B. $ (8 - x)(10 - x) = 8×10 + 40 $
C. $ (8 + x)(10 + x) = 8×10 - 40 $
D. $ (8 + x)(10 + x) = 8×10 + 40 $

答案： D

6. 李大爷种植的某种蔬菜计划以每千克5元的价格对外批发销售，由于部分菜农扩大种植面积，造成该种蔬菜滞销。为了尽快销售、减少损失，李大爷对价格经过两次下调后，以每千克3.2元的价格对外批发销售，则平均每次下调的百分率为（D）
A. 6%
B. 8%
C. 10%
D. 20%

答案： D

7. 经过两次连续降价，某药品销售单价由原来的150元降到96元，设该药品平均每次降价的百分率为x，根据题意可列方程是$ 150(1 - x)^2 = 96 $。

答案： $ 150(1 - x)^2 = 96 $