《2025年假期面对面南方出版社八年级数学沪科版》

11.(天津中考)直线$y=2x-1$与x轴交点的坐标为$(\frac{1}{2},0)$.

答案： $(\frac{1}{2},0)$

12.(上海中考)已知正比例函数$y=kx$(k是常数,$k≠0)$的图象经过第二、四象限,那么y的值随着x的值增大而减小(填“增大”或“减小”).

答案： 减小

13.(东营中考)已知一次函数$y=kx+b(k≠0)$的图象经过$A(1,-1),B(-1,3)$两点,则k＜0(填“＞”或“＜”).

答案： ＜

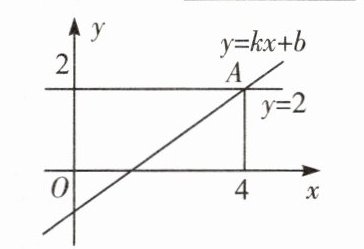
14.(遵义中考)如图,直线$y=kx+b$(k,b是常数,$k≠0)$与直线$y=2$交于点$A(4,2)$,则关于x的不等式$kx+b＜2$的解集为$x ＜ 4$.

答案： $x ＜ 4$

15.(西宁中考)若点$A(m,n)$在直线$y=kx(k≠0)$上,当$-1≤m≤1$时,$-1≤n≤1$,则这条直线的函数表达式为$y = x$ 或 $y = -x$.

答案： $y = x$ 或 $y = -x$

16.(郴州中考)小红在练习仰卧起坐,本月1日至4日的成绩与日期具有如下关系:
|日期x(日)|1|2|3|4|
|----|----|----|----|----|
|成绩y(个)|40|43|46|49|
小红的仰卧起坐成绩y与日期x之间近似为一次函数关系,则该函数表达式为$y = 3x + 37$.

答案： $y = 3x + 37$

17.(10分)(南通中考)如图,直线$l_{1}:y=x+3$与过点$A(3,0)$的直线$l_{2}$交于点$C(1,m)$,与x轴交于点B.
(1)求直线$l_{2}$的表达式;
(2)点M在直线$l_{1}$上,$MN// y$轴,交直线$l_{2}$于点N,若$MN=AB$,求点M的坐标.
(1)直线$l_{2}$的表达式为$y=-2x+6$。
(2)点M的坐标为$(3,6)$或$(-1,2)$。

答案： 解：
(1)在 $y = x + 3$ 中，令 $y = 0$，得 $x = -3$，$\therefore B(-3,0)$。把 $x = 1$ 代入 $y = x + 3$ 得 $y = 4$，$\therefore C(1,4)$。设直线 $l_2$ 的表达式为 $y = kx + b$，则有 $\begin{cases}k + b = 4,\\3k + b = 0,\end{cases}$ 解得 $\begin{cases}k = -2,\\b = 6.\end{cases}$ $\therefore$ 直线 $l_2$ 的表达式为 $y = -2x + 6$。
(2)$AB = 3 - (-3) = 6$，设 $M(a,a + 3)$，由 $MN// y$ 轴，得 $N(a,-2a + 6)$，$MN = |a + 3 - (-2a + 6)| = AB = 6$，解得 $a = 3$ 或 $a = -1$，$\therefore M(3,6)$ 或 $(-1,2)$。

18.(12分)(绵阳中考)4月23日是“世界读书日”,甲、乙两个书店在这一天举行了购书优惠活动.甲书店:所有书籍按标价8折出售;乙书店:一次购书中标价总额不超过100元的按原价计费,超过100元后的部分打6折.
(1)以x(单位:元)表示标价总额,y(单位:元)表示应支付金额,分别就两家书店的优惠方式,求y关于x的函数表达式;
(2)“世界读书日”这一天,如何选择这两家书店去购书更省钱?

答案： 解：
(1)由题意得，甲书店：$y = 0.8x$，乙书店：$y = \begin{cases}x(x\leqslant 100),\\0.6x + 40(x ＞ 100).\end{cases}$
(2)令 $0.8x = 0.6x + 40$，解得 $x = 200$。当 $x ＜ 200$ 时，选择甲书店更省钱；当 $x = 200$ 时，甲、乙书店所需费用相同；当 $x ＞ 200$ 时，选择乙书店更省钱。

19.(14分)(吉林中考)甲、乙两车分别从A,B两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到B地,乙车立即以原速原路返回到B地,甲、乙两车距B地的路程y(km)与各自行驶的时间x(h)之间的关系如图所示.
(1)$m=$4,$n=$120;
(2)求乙车距B地的路程y关于x的函数表达式,并写出自变量x的取值范围;
(3)当甲车到达B地时,求乙车距B地的路程.

答案： 解：
(1)4 120
(2)当 $0\leqslant x\leqslant 2$ 时，设 $y_{乙} = kx(k\neq 0)$。将 $(2,120)$ 代入 $y = kx$，得 $120 = 2k$，$\therefore k = 60$，$\therefore y_{乙} = 60x$。当 $2 ＜ x\leqslant 4$ 时，设 $y_{乙} = k'x + b(k'\neq 0)$。将 $(2,120)$，$(4,0)$ 代入 $y_{乙} = k'x + b$，得 $\begin{cases}120 = 2k' + b,\\0 = 4k' + b,\end{cases}$ 解得 $\begin{cases}k' = -60,\\b = 240,\end{cases}$ $\therefore y_{乙} = -60x + 240$。综上，$y_{乙} = \begin{cases}60x(0\leqslant x\leqslant 2),\\-60x + 240(2 ＜ x\leqslant 4).\end{cases}$
(3)将 $x = 3.5$ 代入 $y = -60x + 240$，得 $y = -60\times 3.5 + 240 = 30$。即当甲车到达 $B$ 地时，乙车距 $B$ 地 $30\ \text{km}$。