《2025年学练考精品单元卷八年级数学全一册北师大版》

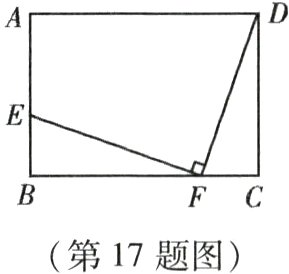
17. (本小题8分)如图,在长方形ABCD中,点E在边AB上,点F在边BC上,且BE = CF,EF⊥DF,求证:BF = CD.

答案： 证明:
∵四边形ABCD是长方形，
∴∠B=∠C=90°.
∵EF⊥DF,
∴∠EFD=90°,
∴∠EFB+∠CFD=90°.
∵∠EFB+∠BEF=90°,
∴∠BEF=∠CFD.
　　　　　　　　　　　∠BEF=CFD,
　在△BEF和△CFD中，{BE=CF,
　　　　　　　　　　　∠B=∠C,
∴△BEF≌△CFD(ASA),
∴BF=CD.

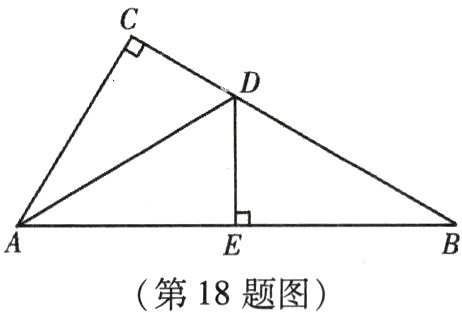
18. (本小题9分)如图,在△ABC中,∠C = 90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:△ACD≌△AED;
(2)若∠B = 30°,CD = 1,求BD的长.

答案：
(1)证明:
∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=ED,∠DEA=∠C=90°.
∵在Rt△ACD和Rt△AED中{ACDD==ADDE
∴Rt△ACD≌Rt△AED(HL);
(2)解:
∵DE⊥AB,
∴∠DEB=90°.
∵DE=DC=1,∠B=30°,
∴BD=2DE=2.

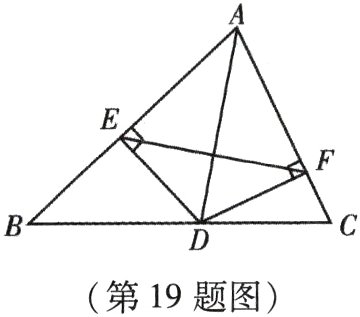
19. (本小题8分)如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF.
求证:AD垂直平分EF.

答案： 证明:
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∴点D在线段EF的垂直平分线上.在
Rt△ADE和Rt△ADF中,{ADDE==ADDF,,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
∴点A在线段EF的垂直平分线上.
∵两点确定一条直线，
∴AD垂直平分EF:

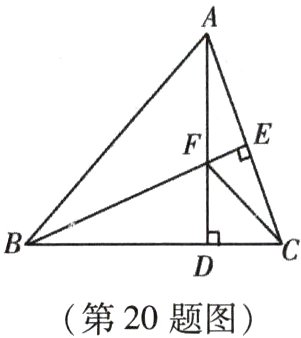
20. (本小题10分)如图,△ABC中,AB = BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD = 45°,AD与BE交于点F,连接CF.
(1)求证:BF = 2AE;
(2)若CD = $\sqrt{2}$,求AD的长.

答案：
(1)证明:
∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形，
∴AD=BD.
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,在△ADC和△BDF中，
　∠CAD=∠CBE
{AD=BD
　
　
　
∴△ADC≌△BDF(ASA),∠ADC=∠BDF=90°
∴BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
(2)解:
∵△ADC≌△BDF,
∴DF=CD=√2;
在Rt△CDF中,CF=　$\sqrt{DF²+CD²}$
=　$\sqrt{(√2)²+(√2)²}$=2,
∵BE⊥AC,AE=EC,
∴AF=CF=2,
∴AD=AF+DF=2+√2;