16. (本小题8分)如图所示,将四边形ABCD绕O点按逆时针方向旋转后得到一个四边形,请在图中依次标上点A,B,C,D的对应点E,F,G,H.
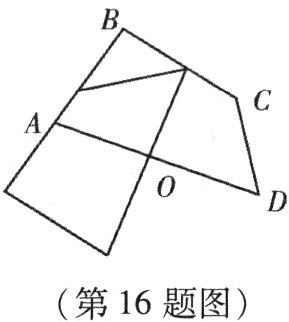

答案:
解:如图所示:

解:如图所示:

17. (本小题8分)在图中作出“三角旗”绕O点按逆时针旋转90°后的图案.
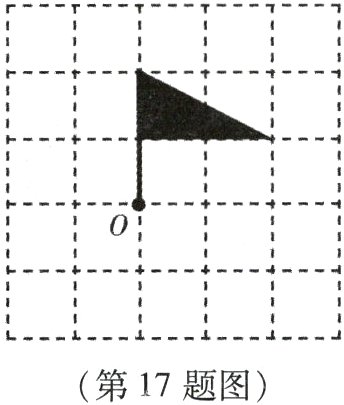

答案:
解:如图所示:

解:如图所示:

18. (本小题9分)如图,在10×10的正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A₁B₁C₁,再把△A₁B₁C₁向右平移3个单位,得到△A₂B₂C₂,再将△A₂B₂C₂绕点C₂顺时针旋转90°,得到△A₃B₃C₃,请你在图中画出△A₁B₁C₁,△A₂B₂C₂和△A₃B₃C₃(不要求写画法).
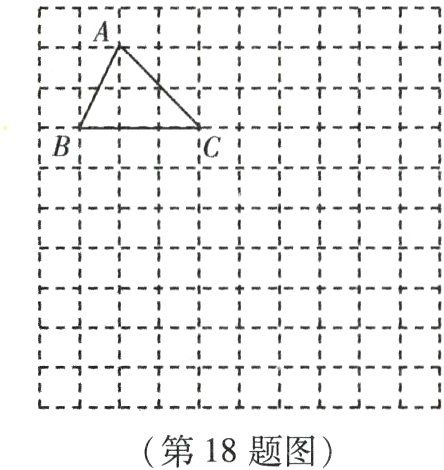

答案:
解:如图所示:

解:如图所示:

19. (本小题8分)如图所示,已知P为正方形ABCD外的一点.PA = 1,PB = 2.将△ABP绕点B顺时针旋转90°,使点P旋转至点P',且AP' = 3,求∠BP'C的度数.
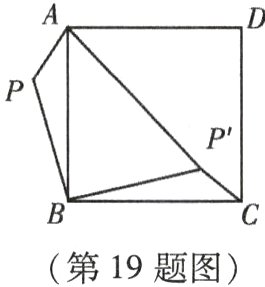

答案:
解:连接 $ PP' $,

$\because BP = BP' = 2$,$\therefore PP' = 2\sqrt{2}$,$AP = 1$,$AP' = 3$,
根据勾股定理得,$\angle APP' = 90^{\circ}$,$\angle BPP' = 45^{\circ}$,
$\therefore \angle APB = 135^{\circ}$,$\angle BP'C = 135^{\circ}$.
解:连接 $ PP' $,

$\because BP = BP' = 2$,$\therefore PP' = 2\sqrt{2}$,$AP = 1$,$AP' = 3$,
根据勾股定理得,$\angle APP' = 90^{\circ}$,$\angle BPP' = 45^{\circ}$,
$\therefore \angle APB = 135^{\circ}$,$\angle BP'C = 135^{\circ}$.
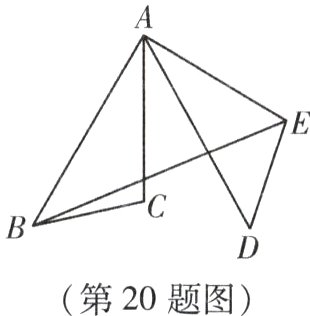
20. (本小题8分)如图,在△ABC中,AB = $\sqrt{5}$,AC = 2,∠BAC = 30°,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,求BE的长.

答案:
解:$\because$将$\triangle ABC$绕点$A$逆时针旋转$60^{\circ}$,得到$\triangle ADE$,
$\therefore \angle CAE = 60^{\circ}$,$AC = AE = 2$,
$\because \angle BAC = 30^{\circ}$,$\therefore \angle BAE = \angle BAC + \angle CAE = 90^{\circ}$,
$\therefore BE = \sqrt{AB^{2} + AE^{2}} = \sqrt{5 + 4} = 3$.
$\therefore \angle CAE = 60^{\circ}$,$AC = AE = 2$,
$\because \angle BAC = 30^{\circ}$,$\therefore \angle BAE = \angle BAC + \angle CAE = 90^{\circ}$,
$\therefore BE = \sqrt{AB^{2} + AE^{2}} = \sqrt{5 + 4} = 3$.
查看更多完整答案,请扫码查看


