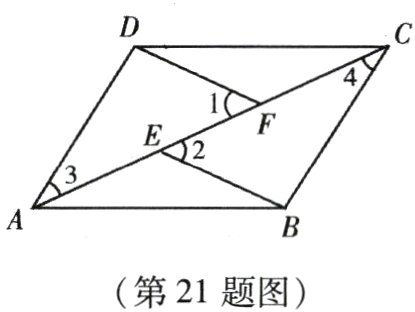
21. (本小题10分)已知:如图,E,F是四边形ABCD的对角线AC上的两点,AF = CE,DF = BE,DF//BE. 求证:
(1) △AFD≌△CEB;
(2) 四边形ABCD是平行四边形.
(1) △AFD≌△CEB;
(2) 四边形ABCD是平行四边形.

答案:
证明:
(1)$\because DF// BE$,$\therefore \angle 1 = \angle 2$.
$\because AF = CE$,$DF = BE$,$\therefore \triangle AFD\cong\triangle CEB(SAS)$.
(2)$\because \triangle AFD\cong\triangle CEB$,$\therefore \angle 3 = \angle 4$,$AD = BC$,
$\therefore AD// BC$. $\therefore$四边形$ABCD$是平行四边形.
(1)$\because DF// BE$,$\therefore \angle 1 = \angle 2$.
$\because AF = CE$,$DF = BE$,$\therefore \triangle AFD\cong\triangle CEB(SAS)$.
(2)$\because \triangle AFD\cong\triangle CEB$,$\therefore \angle 3 = \angle 4$,$AD = BC$,
$\therefore AD// BC$. $\therefore$四边形$ABCD$是平行四边形.
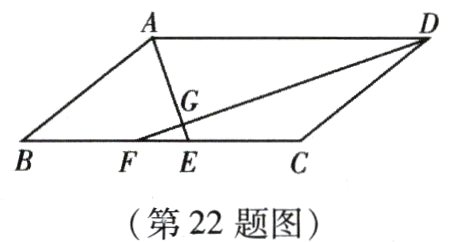
22. (本小题10分)已知:如图,在□ABCD中,∠ADC、∠DAB的平分线DF、AE分别与线段BC相交于点F、E,DF与AE相交于点G.
(1) 求证:AE⊥DF;
(2) 若AD = 10,AB = 6,AE = 4,求DF的长.
(1) 求证:AE⊥DF;
(2) 若AD = 10,AB = 6,AE = 4,求DF的长.

答案:
(1)证明:在$\square ABCD$中$AB// CD$,
$\therefore \angle ADC+\angle DAB = 180^{\circ}$.
$\because DF$、$AE$分别是$\angle ADC$、$\angle DAB$的平分线,
$\therefore \angle ADF = \angle CDF=\frac{1}{2}\angle ADC$,
$\angle DAE = \angle BAE=\frac{1}{2}\angle DAB$,
$\therefore \angle ADF+\angle DAE=\frac{1}{2}(\angle ADC+\angle DAB)=90^{\circ}$,
$\therefore \angle AGD = 90^{\circ}$,$\therefore AE\perp DF$.
(2)解:过点$D$作$DH// AE$,交$BC$的延长线于点$H$,
则四边形$AEHD$是平行四边形,且$FD\perp DH$.

$\therefore DH = AE = 4$,$EH = AD = 10$. 在$\square ABCD$中$AD// BC$,
$\therefore \angle ADF = \angle CFD$,$\angle DAE = \angle BEA$.
$\therefore \angle CDF = \angle CFD$,$\angle BAE = \angle BEA$.
$\therefore DC = FC$,$AB = EB$. 在$\square ABCD$中,$AD = BC = 10$,$AB = DC = 6$,$\therefore CF = BE = 6$,
$BF = BC - CF = 10 - 6 = 4$.
$\therefore FE = BE - BF = 6 - 4 = 2$,
$\therefore FH = FE + EH = 12$,
在$Rt\triangle FDH$中,
$DF = \sqrt{FH^{2}-DH^{2}}=\sqrt{12^{2}-4^{2}} = 8\sqrt{2}$.
(1)证明:在$\square ABCD$中$AB// CD$,
$\therefore \angle ADC+\angle DAB = 180^{\circ}$.
$\because DF$、$AE$分别是$\angle ADC$、$\angle DAB$的平分线,
$\therefore \angle ADF = \angle CDF=\frac{1}{2}\angle ADC$,
$\angle DAE = \angle BAE=\frac{1}{2}\angle DAB$,
$\therefore \angle ADF+\angle DAE=\frac{1}{2}(\angle ADC+\angle DAB)=90^{\circ}$,
$\therefore \angle AGD = 90^{\circ}$,$\therefore AE\perp DF$.
(2)解:过点$D$作$DH// AE$,交$BC$的延长线于点$H$,
则四边形$AEHD$是平行四边形,且$FD\perp DH$.

$\therefore DH = AE = 4$,$EH = AD = 10$. 在$\square ABCD$中$AD// BC$,
$\therefore \angle ADF = \angle CFD$,$\angle DAE = \angle BEA$.
$\therefore \angle CDF = \angle CFD$,$\angle BAE = \angle BEA$.
$\therefore DC = FC$,$AB = EB$. 在$\square ABCD$中,$AD = BC = 10$,$AB = DC = 6$,$\therefore CF = BE = 6$,
$BF = BC - CF = 10 - 6 = 4$.
$\therefore FE = BE - BF = 6 - 4 = 2$,
$\therefore FH = FE + EH = 12$,
在$Rt\triangle FDH$中,
$DF = \sqrt{FH^{2}-DH^{2}}=\sqrt{12^{2}-4^{2}} = 8\sqrt{2}$.
23. (本小题12分)我们新定义一种三角形:两边平方和等于第三边平方的3倍的三角形叫做非凡三角形. 例如:某三角形三边长分别是√3,2和3,因为(√3)² + 3² = 12 = 3×2²,所以这个三角形是非凡三角形.
(1) 若△ABC是非凡三角形,且AB = 3,BC = 6,则AC = _______;
(2) 如图,在□ABCD中,AC⊥BD于点O,AB = 6,且△ABD是非凡三角形,求AC的值.
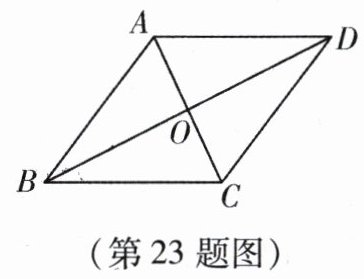
(1) 若△ABC是非凡三角形,且AB = 3,BC = 6,则AC = _______;
(2) 如图,在□ABCD中,AC⊥BD于点O,AB = 6,且△ABD是非凡三角形,求AC的值.

答案:
解:
(1)$\sqrt{15}$;
(2)$\because$四边形$ABCD$是平行四边形,
$\therefore BO = DO=\frac{1}{2}BD$,又$\because AC\perp BD$,
$\therefore AC$垂直平分$BD$,$\therefore AD = AB = 6$,
$\because \triangle ABD$是非凡三角形,
①当$AB^{2}+AD^{2}=3BD^{2}$时,
则$BD^{2}=\frac{1}{3}(AB^{2}+AD^{2}) = 24$,$\therefore BD = 2\sqrt{6}$,
$\therefore BO=\frac{1}{2}BD=\sqrt{6}$,
在$Rt\triangle AOB$中,$AO = \sqrt{AB^{2}-BO^{2}}=\sqrt{30}$,
$\therefore AC = 2AO = 2\sqrt{30}$;
②当$AB^{2}+BD^{2}=3AD^{2}$时,
则$BD^{2}=3AD^{2}-AB^{2}=2AD^{2}=72$,
$\therefore BD = 6\sqrt{2}$,$\therefore BO=\frac{1}{2}BD = 3\sqrt{2}$,
在$Rt\triangle AOB$中,$AO = \sqrt{AB^{2}-BO^{2}} = 3\sqrt{2}$.
$\therefore AC = 2AO = 6\sqrt{2}$;
③当$AD^{2}+BD^{2}=3AB^{2}$时,与②情况相同;
综上所述,$AC$的值为$2\sqrt{30}$或$6\sqrt{2}$.
(1)$\sqrt{15}$;
(2)$\because$四边形$ABCD$是平行四边形,
$\therefore BO = DO=\frac{1}{2}BD$,又$\because AC\perp BD$,
$\therefore AC$垂直平分$BD$,$\therefore AD = AB = 6$,
$\because \triangle ABD$是非凡三角形,
①当$AB^{2}+AD^{2}=3BD^{2}$时,
则$BD^{2}=\frac{1}{3}(AB^{2}+AD^{2}) = 24$,$\therefore BD = 2\sqrt{6}$,
$\therefore BO=\frac{1}{2}BD=\sqrt{6}$,
在$Rt\triangle AOB$中,$AO = \sqrt{AB^{2}-BO^{2}}=\sqrt{30}$,
$\therefore AC = 2AO = 2\sqrt{30}$;
②当$AB^{2}+BD^{2}=3AD^{2}$时,
则$BD^{2}=3AD^{2}-AB^{2}=2AD^{2}=72$,
$\therefore BD = 6\sqrt{2}$,$\therefore BO=\frac{1}{2}BD = 3\sqrt{2}$,
在$Rt\triangle AOB$中,$AO = \sqrt{AB^{2}-BO^{2}} = 3\sqrt{2}$.
$\therefore AC = 2AO = 6\sqrt{2}$;
③当$AD^{2}+BD^{2}=3AB^{2}$时,与②情况相同;
综上所述,$AC$的值为$2\sqrt{30}$或$6\sqrt{2}$.
查看更多完整答案,请扫码查看


