《2025年学练考精品单元卷八年级数学全一册北师大版》

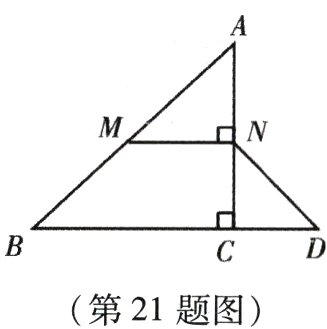
21.(本小题10分)如图,在△ABC中,∠ACB = 90°,M,N分别是AB,AC的中点,延长BC至点D,使CD = $\frac{1}{3}$BD,连接DN,MN.若AB = 6.
(1)求证:MN = CD;
(2)求DN的长.

答案： 解:
(1)证明:
∵M,N分别是AB,AC的中点，
∴MN//BC,MN=$\frac{1}{2}$BC.
∵CD=$\frac{1}{3}$BD,
∴CD=$\frac{1}{2}$BC,
∴MN=CD.
(2)连接CM,由
(1)知MN//CD,MN=CD,
∴四边形MCDN是平行四边形，
∴DN=CM.
∵∠ACB=90°,M是AB的中点，
∴CM=$\frac{1}{2}$AB,
∴DN=$\frac{1}{2}$AB =3.

22.(本小题10分)如图,点E、F是▱ABCD对角线AC上的两点,且AE = CF,连接BE、DE、BF、DF.
(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥BF,AB = 8,BF = 6,AC = 16,求△ABC的面积.

答案：
(1)证明:
∵四边形ABCD是平行四边形，
∴AD=CB,AD//CB,
∴∠BCE=∠DAF,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
∴△ADF≌△CBE(SAS),△AED≌△CFB(SAS)
∴DF=BE,BF=DE
∴四边形BEDF是平行四边形:
(2)解:
∵AB⊥BF,AB=8,BF=6.
∴AF=$\sqrt{AB^{2}+BF^{2}}$=10,
∵AC=16,
∴$\frac{S_{\triangle ABC}}{S_{\triangle ABF}}$=$\frac{AC}{AF}$=$\frac{8}{5}$(同高三角形)，
∵S_{\triangle ABF}=$\frac{1}{2}$AB·BF=$\frac{1}{2}$×6×8=24,
∴S_{\triangle ABC}=$\frac{8}{5}$S_{\triangle ABF}=$\frac{192}{5}$.

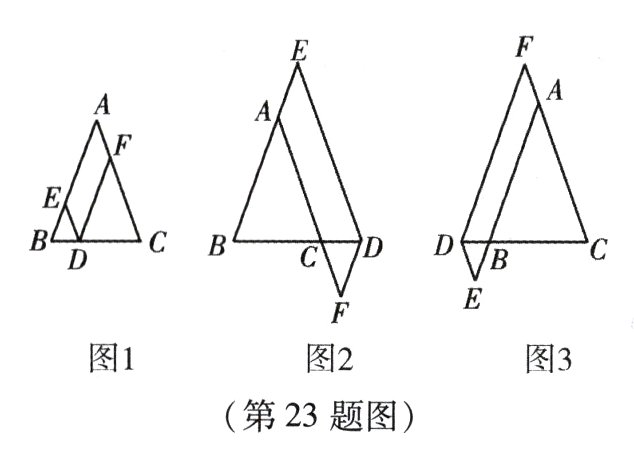
23.(本小题12分)如图,在△ABC中,AB = AC,点D在边BC所在的直线上,过点D作DE//AC交直线AB于点E,DF//AB交直线AC于点F.
(1)当点D在边BC上时,如图1,求证:DE + DF = AC;
(2)当点D在边BC的延长线上时,如图2;当点D在边BC的反向延长线上时,如图3.请分别写出图2、图3中DE,DF,AC之间的数量关系,不需要证明;
(3)若AC = 6,DE = 4,则DF = __________.

答案： 解:
(1)证明:
∵DE//AC,DF//AB,
∴四边形AEDF是平行四边形，
∴DE=AF.
∵AB=AC,
∴∠B=∠C.
∵DF//AB,
∴∠CDF=∠B,
∴∠CDF=∠C,
∴DF=CF,
∴DE+DF=AF+CF=AC.
(2)当点D在边BC的延长线上时,DE−DF=AC;当点D在边BC的反向延长线上时,DF−DE=AC.
(3)2或10