8. 在Rt△ABC中,∠C = 90°,AC = 9,BC = 12,则点C到AB的距离是( )
A. $\frac{36}{5}$
B. $\frac{12}{25}$
C. $\frac{9}{4}$
D. $\frac{3\sqrt{3}}{4}$
A. $\frac{36}{5}$
B. $\frac{12}{25}$
C. $\frac{9}{4}$
D. $\frac{3\sqrt{3}}{4}$
答案:
A
9. 如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE = DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
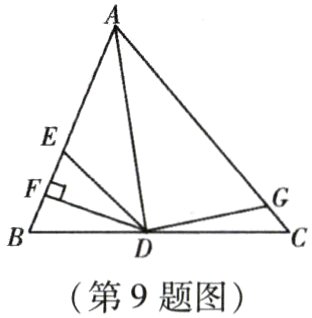
A. 11
B. 5.5
C. 7
D. 3.5

A. 11
B. 5.5
C. 7
D. 3.5
答案:
B
10. 如图,已知∠MON = 30°,点A₁、A₂、A₃…在射线ON上,点B₁、B₂、B₃…在射线OM上,△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄…均为等边三角形,若OA₁ = 1,则△A₆B₆A₇的边长为( )

A. 6
B. 12
C. 32
D. 64

A. 6
B. 12
C. 32
D. 64
答案:
C
11. 用反证法证明“一个三角形中不可能有两个角是直角”时,第一步应假设一个三角形中有两个角是直角.
答案:
三角形中有两个角是直角
12. 如图,在Rt△ABC中,∠ACB = 90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F = 30°,DE = 1,则BE的长是________.
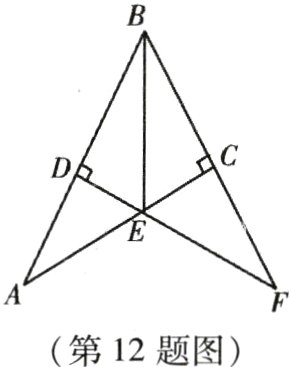

答案:
2
13. 如图,在△ABC中,BC = 5 cm,BP,CP分别是∠ABC和∠ACB的角平分线,且PD//AB,PE//AC,则△PDE的周长是________ cm.
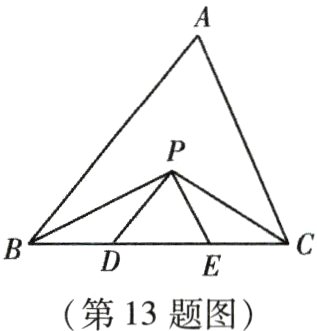

答案:
5
14. 如图,在Rt△ABC中,∠C = 90°,AD平分∠CAB,CD = 3,AB = 12,则△ABD的面积为________.


答案:
18
15. 如图所示,∠BOC = 60°,A是BO延长线上的一点,OA = 10 cm,动点P从点A出发沿AB以2 cm/s的速度移动,动点Q从点O出发沿OC以1 cm/s的速度移动,如果点P,Q同时出发,用t(s)表示移动的时间,当t = ________ s时,△POQ是等腰三角形.
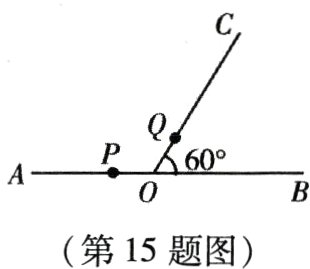

答案:
$\frac{10}{3}$或10
16. (本小题8分)如图,校园有两条路OA、OB,在交叉口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你用尺规作出灯柱的位置点P.(请保留作图痕迹)
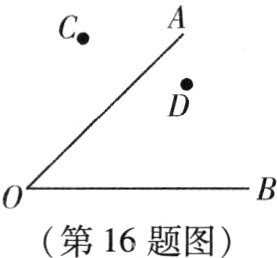

答案:
解:连接CD.作CD的垂直平分线,作∠A0B的角平分线,两线交于P,此时点P为所求灯柱位置,如图所示:

解:连接CD.作CD的垂直平分线,作∠A0B的角平分线,两线交于P,此时点P为所求灯柱位置,如图所示:

查看更多完整答案,请扫码查看


