17. (本小题8分)已知□ABCD的周长为40 cm,AB:BC = 2:3,求CD和AD的长.
答案:
解:$\because$四边形$ABCD$是平行四边形,
$\therefore AB = CD$,$AD = BC$. 设$AB = CD = 2a\ cm$,$AD = BC = 3a\ cm$,
又$\because$平行四边形$ABCD$的周长为$40\ cm$,
$\therefore 2(2a + 3a)= 40$,解得$a = 4$,
$\therefore CD = 8\ cm$,$AD = 12\ cm$.
$\therefore AB = CD$,$AD = BC$. 设$AB = CD = 2a\ cm$,$AD = BC = 3a\ cm$,
又$\because$平行四边形$ABCD$的周长为$40\ cm$,
$\therefore 2(2a + 3a)= 40$,解得$a = 4$,
$\therefore CD = 8\ cm$,$AD = 12\ cm$.
18. (本小题8分)如图,已知BD是△ABC的角平分线,点E,F分别在边AB,BC上,ED//BC,EF//AC. 求证:BE = CF.
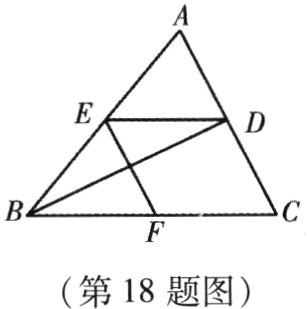

答案:
证明:$\because ED// BC$,$EF// AC$,
$\therefore$四边形$EFCD$是平行四边形,$\therefore ED = CF$.
$\because BD$平分$\angle ABC$,$\therefore \angle EBD = \angle DBC$.
$\because ED// BC$,$\therefore \angle EDB = \angle DBC$,
$\therefore \angle EBD = \angle EDB$,$\therefore BE = ED$,$\therefore BE = CF$.
$\therefore$四边形$EFCD$是平行四边形,$\therefore ED = CF$.
$\because BD$平分$\angle ABC$,$\therefore \angle EBD = \angle DBC$.
$\because ED// BC$,$\therefore \angle EDB = \angle DBC$,
$\therefore \angle EBD = \angle EDB$,$\therefore BE = ED$,$\therefore BE = CF$.
19. (本小题9分)如图,四边形ABCD是平行四边形,AD = 12,AB = 13,BD⊥AD,求BC,CD及OB的长.
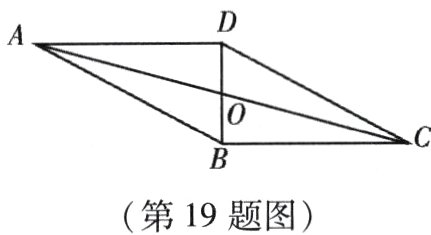

答案:
解:$\because$四边形$ABCD$是平行四边形,
$\therefore BC = AD = 12$,$CD = AB = 13$,$OB=\frac{1}{2}BD$.
$\because BD\perp AD$,$\therefore BD = \sqrt{AB^{2}-AD^{2}}=\sqrt{13^{2}-12^{2}} = 5$,
$\therefore OB=\frac{1}{2}BD=\frac{5}{2}$.
$\therefore BC = AD = 12$,$CD = AB = 13$,$OB=\frac{1}{2}BD$.
$\because BD\perp AD$,$\therefore BD = \sqrt{AB^{2}-AD^{2}}=\sqrt{13^{2}-12^{2}} = 5$,
$\therefore OB=\frac{1}{2}BD=\frac{5}{2}$.
20. (本小题10分)如图,在□ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形. 求证:四边形ABOE是平行四边形.
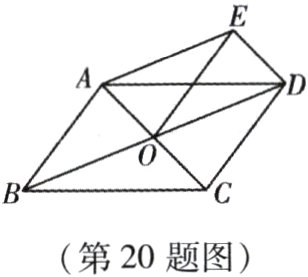

答案:
解:$\because$在平行四边形$ABCD$中,
对角线$AC$交$BD$于点$O$,$\therefore OB = OD$.
又$\because$四边形$AODE$是平行四边形,
$\therefore AE// OD$,$AE = OD$,$\therefore AE// OB$,$AE = OB$,
$\therefore$四边形$ABOE$是平行四边形.
对角线$AC$交$BD$于点$O$,$\therefore OB = OD$.
又$\because$四边形$AODE$是平行四边形,
$\therefore AE// OD$,$AE = OD$,$\therefore AE// OB$,$AE = OB$,
$\therefore$四边形$ABOE$是平行四边形.
查看更多完整答案,请扫码查看


