9. 如图,过□ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的□AEMG的面积S₁与□HCFM的面积S₂的大小关系是( )

A. S₁ > S₂
B. S₁ < S₂
C. S₁ = S₂
D. 2S₁ = S₂

A. S₁ > S₂
B. S₁ < S₂
C. S₁ = S₂
D. 2S₁ = S₂
答案:
C
10. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB = AE,延长AB与DE的延长线交于点F,下列结论中:①△ABC≌△ADE;②△ABE是等边三角形;③AD = AF;④S△ABE = S△CDE;⑤S△ABE = S△CEF. 其中正确的是( )
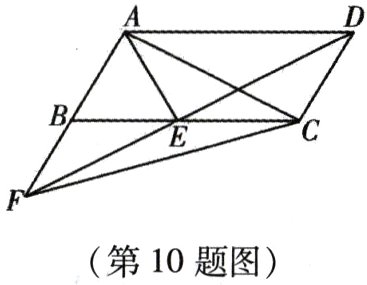
A. ①②③
B. ①②④
C. ①②⑤
D. ①③④

A. ①②③
B. ①②④
C. ①②⑤
D. ①③④
答案:
C
11. 如图,在□ABCD中,AD = 8,点E,F分别是BD,CD的中点,则EF = _______.
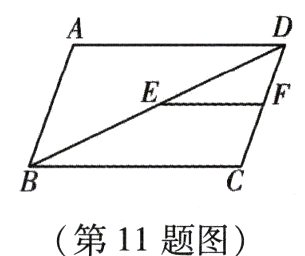

答案:
4
12. 如图,∠1,∠2,∠3,∠4是五边形ABCDE的4个外角,若∠A = 120°,则∠1 + ∠2 + ∠3 + ∠4 = _______°.
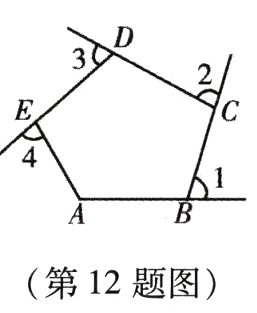

答案:
300
13. 如图,在四边形ABCD中,AD//BC,且AD > BC,BC = 6 cm,动点P,Q分别从A,C同时出发,点P以1 cm/s的速度由A向D运动,点Q以2 cm/s的速度由C向B运动,则经过_______s后四边形ABQP为平行四边形.
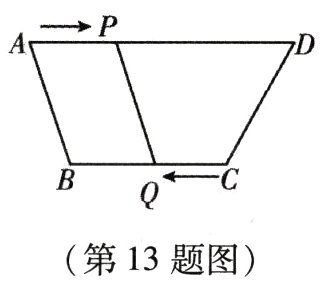

答案:
2
14. 如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF = 45°,且AE + AF = 2√2,则平行四边形ABCD的周长是_______.


答案:
8
15. 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G. 若∠BAC = 30°,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD = 4AG;④△DBF≌△EFA. 其中正确结论的序号是_______.
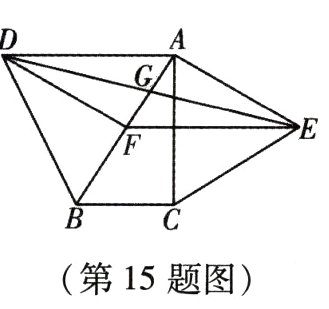

答案:
①②③④
16. (本小题8分)一个正多边形的一个内角减去与它相邻的一个外角的结果为90°,求这个多边形的边数和内角和的度数.
答案:
解:设每一个外角为$x^{\circ}$,
则每一个内角为$(x + 90)^{\circ}$,
根据题意,得$x + x + 90 = 180$,解得$x = 45$.
$\therefore 360\div45 = 8$,$\therefore (8 - 2)\times180^{\circ}= 1080^{\circ}$.
则这个多边形的内角和为$1080^{\circ}$,它的边数为 8.
则每一个内角为$(x + 90)^{\circ}$,
根据题意,得$x + x + 90 = 180$,解得$x = 45$.
$\therefore 360\div45 = 8$,$\therefore (8 - 2)\times180^{\circ}= 1080^{\circ}$.
则这个多边形的内角和为$1080^{\circ}$,它的边数为 8.
查看更多完整答案,请扫码查看


