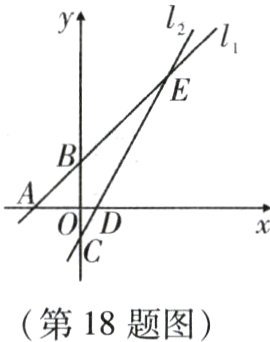
18. (本小题8分)如图,直线l₁的函数表达式为y = x + 1,且l₁分别交x轴、y轴于点A,B. 直线l₂的函数表达式为y = kx + b,l₂经过点C(0, - 1),分别交x轴、直线l₁于点D,E,且E点坐标为(n,3).
(1)求k和b的值;
(2)求△ADE的面积;
(3)直接写出不等式kx + b>x + 1的解集.
(1)求k和b的值;
(2)求△ADE的面积;
(3)直接写出不等式kx + b>x + 1的解集.

答案:
解:把$(n,3)$代入$y = x + 1$得:$3 = n + 1$,解得:$n = 2$,$\therefore E(2,3)$,把$E(2,3)$,$C(0,-1)$代入$y = kx + b$得:$\begin{cases}2k + b = 3\\b = - 1\end{cases}$,解得:$\begin{cases}k = 2\\b = - 1\end{cases}$;
(2) 当$y = x + 1 = 0$时,解得:$x = - 1$,$\therefore A(-1,0)$,由
(1)知直线$l_{2}$的函数表达式为$y = 2x - 1$,当$y = 0$时,即$2x - 1 = 0$,解得:$x=\dfrac{1}{2}$,$\therefore D(\dfrac{1}{2},0)$,$\because E(2,3)$,$\therefore S_{\triangle ADE}=\dfrac{1}{2}\times(\dfrac{1}{2}+1)\times3=\dfrac{9}{4}$;
(3)$\because E(2,3)$,$\therefore$由函数图象可得不等式$kx + b>x + 1$的解集为$x>2$.
(2) 当$y = x + 1 = 0$时,解得:$x = - 1$,$\therefore A(-1,0)$,由
(1)知直线$l_{2}$的函数表达式为$y = 2x - 1$,当$y = 0$时,即$2x - 1 = 0$,解得:$x=\dfrac{1}{2}$,$\therefore D(\dfrac{1}{2},0)$,$\because E(2,3)$,$\therefore S_{\triangle ADE}=\dfrac{1}{2}\times(\dfrac{1}{2}+1)\times3=\dfrac{9}{4}$;
(3)$\because E(2,3)$,$\therefore$由函数图象可得不等式$kx + b>x + 1$的解集为$x>2$.
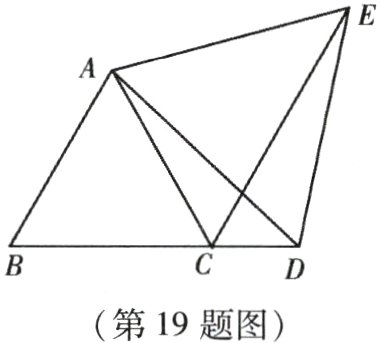
19. (本小题8分)如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE = BD,求证:△ADE为等边三角形.

答案:
证明:$\because\triangle ABC$为等边三角形,$\therefore\angle B=\angle ACB = 60^{\circ}$,$AB = AC$,即$\angle ACD = 120^{\circ}$. $\because CE$平分$\angle ACD$,$\therefore\angle 1=\angle 2 = 60^{\circ}$.
在$\triangle ABD$和$\triangle ACE$中,$\begin{cases}AB = AC\\\angle B=\angle 1\\BD = CE\end{cases}$,$\therefore\triangle ABD\cong\triangle ACE(SAS)$,$\therefore AD = AE$,$\angle BAD=\angle CAE$,又$\angle BAC = 60^{\circ}$,$\therefore\angle DAE = 60^{\circ}$,$\therefore\triangle ADE$为等边三角形.

证明:$\because\triangle ABC$为等边三角形,$\therefore\angle B=\angle ACB = 60^{\circ}$,$AB = AC$,即$\angle ACD = 120^{\circ}$. $\because CE$平分$\angle ACD$,$\therefore\angle 1=\angle 2 = 60^{\circ}$.
在$\triangle ABD$和$\triangle ACE$中,$\begin{cases}AB = AC\\\angle B=\angle 1\\BD = CE\end{cases}$,$\therefore\triangle ABD\cong\triangle ACE(SAS)$,$\therefore AD = AE$,$\angle BAD=\angle CAE$,又$\angle BAC = 60^{\circ}$,$\therefore\angle DAE = 60^{\circ}$,$\therefore\triangle ADE$为等边三角形.

20. (本小题9分)某电信公司最近开发A、B两种型号的手机,一经营手机专卖店销售A、B两种型号的手机,上周销售1部A型、3部B型的手机,销售额为8400元. 本周销售2部A型、1部B型的手机,销售额为5800元.
(1)求每部A型和每部B型手机销售价格各是多少元;
(2)如果某单位拟向该店购买A、B两种型号的手机共6部,发给职工联系业务,购手机费用不少于11200元且不多于11600元,问有哪几种购买方案;
(3)在(2)中哪种方案费用更省?最少费用是多少?
(1)求每部A型和每部B型手机销售价格各是多少元;
(2)如果某单位拟向该店购买A、B两种型号的手机共6部,发给职工联系业务,购手机费用不少于11200元且不多于11600元,问有哪几种购买方案;
(3)在(2)中哪种方案费用更省?最少费用是多少?
答案:
解:
(1) 设$A$型手机每部售价$x$元,$B$型手机每部售价$y$元,则$\begin{cases}x + 3y = 8400\\2x + y = 5800\end{cases}$,解得$\begin{cases}x = 1800\\y = 2200\end{cases}$,答:$A$型手机每部售价 1800 元,$B$型手机每部售价 2200 元.
(2) 设购买$A$型手机$a$部,则购买$B$型手机$(6 - a)$部,于是,$11200\leqslant1800a + 2200(6 - a)\leqslant11600$,$\therefore4\leqslant a\leqslant5$,$\because a$为整数,$\therefore a = 4$或 5. 答:有两种购买方案,即方案①:购买$A$型手机 4 部,购买$B$型手机 2 部;方案②:购买$A$型手机 5 部,购买$B$型手机 1 部.
(3) 按方案①购买:$1800\times4 + 2200\times2 = 11600$(元),按方案②购买:$1800\times5 + 2200 = 11200$(元),因此,按方案②购买更省,最少费用是 11200 元.
(1) 设$A$型手机每部售价$x$元,$B$型手机每部售价$y$元,则$\begin{cases}x + 3y = 8400\\2x + y = 5800\end{cases}$,解得$\begin{cases}x = 1800\\y = 2200\end{cases}$,答:$A$型手机每部售价 1800 元,$B$型手机每部售价 2200 元.
(2) 设购买$A$型手机$a$部,则购买$B$型手机$(6 - a)$部,于是,$11200\leqslant1800a + 2200(6 - a)\leqslant11600$,$\therefore4\leqslant a\leqslant5$,$\because a$为整数,$\therefore a = 4$或 5. 答:有两种购买方案,即方案①:购买$A$型手机 4 部,购买$B$型手机 2 部;方案②:购买$A$型手机 5 部,购买$B$型手机 1 部.
(3) 按方案①购买:$1800\times4 + 2200\times2 = 11600$(元),按方案②购买:$1800\times5 + 2200 = 11200$(元),因此,按方案②购买更省,最少费用是 11200 元.
21. (本小题10分)某校长暑假带领该校“三好学生”去旅游,甲旅行社说:“若校长买全票一张,则学生可享受半价优惠. ”乙旅行社说:“包括校长在内都6折优惠. ”若全票价是1200元,则:设学生数为x,甲旅行社收费y₁,乙旅行社收费y₂.
(1)分别写出两家旅行社的收费与学生人数的关系式;
(2)当学生人数是多少时,两家旅行社的收费是一样的?
(3)就学生人数讨论哪家旅行社更优惠.
(1)分别写出两家旅行社的收费与学生人数的关系式;
(2)当学生人数是多少时,两家旅行社的收费是一样的?
(3)就学生人数讨论哪家旅行社更优惠.
答案:
解:
(1) 由题意,得$y_{甲}=0.5\times1200x + 1200 = 600x + 1200$,$y_{乙}=0.6\times1200x + 0.6\times1200 = 720x + 720$;
(2) 当$y_{甲}=y_{乙}$时,$600x + 1200 = 720x + 720$,解得:$x = 4$,故当$x = 4$时,两家旅行社一样优惠;
(3)$y_{甲}>y_{乙}$时,$600x + 1200>720x + 720$,解得:$x < 4$,故当$x < 4$时,乙旅行社优惠. 当$y_{甲}<y_{乙}$时,$600x + 1200<720x + 720$,解得:$x > 4$,故当$x > 4$时,甲旅行社优惠.
(1) 由题意,得$y_{甲}=0.5\times1200x + 1200 = 600x + 1200$,$y_{乙}=0.6\times1200x + 0.6\times1200 = 720x + 720$;
(2) 当$y_{甲}=y_{乙}$时,$600x + 1200 = 720x + 720$,解得:$x = 4$,故当$x = 4$时,两家旅行社一样优惠;
(3)$y_{甲}>y_{乙}$时,$600x + 1200>720x + 720$,解得:$x < 4$,故当$x < 4$时,乙旅行社优惠. 当$y_{甲}<y_{乙}$时,$600x + 1200<720x + 720$,解得:$x > 4$,故当$x > 4$时,甲旅行社优惠.
查看更多完整答案,请扫码查看


