《2025年学练考精品单元卷八年级数学全一册北师大版》

8. 如图，在平面直角坐标系中，$O$为坐标原点，点$A$的坐标为$(1,\sqrt{3})$，$M$为坐标轴上一点，且使得$\triangle MOA$为等腰三角形，则满足条件的点$M$的个数为( )

A. 4个
B. 5个
C. 6个
D. 8个

答案： C

9. 如图，在正方形$ABCD$中，$AB = 6$，点$M$在$CD$的边上，且$DM = 1.5$，$\triangle AEM$与$\triangle ADM$关于$AM$所在的直线对称，将$\triangle ADM$按顺时针方向绕点$A$旋转$90^{\circ}$得到$\triangle ABF$，连接$EF$，则线段$EF$的长为( )

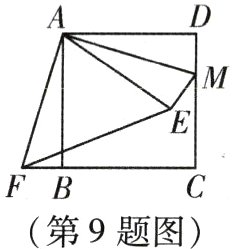
A. $\frac{9}{2}$
B. $\frac{3\sqrt{15}}{2}$
C. $\frac{15}{2}$
D. $\frac{3\sqrt{17}}{2}$

答案： C

10. 如图，在$\triangle ABC$中，$\angle BAC = 90^{\circ}$，$P$是$\triangle ABC$内一点，点$D$，$E$，$F$分别是点$P$关于直线$AC$，$AB$，$BC$的对称点，给出下面三个结论：①$AE = AD$；②$\angle DPE = 90^{\circ}$；③$\angle ADC + \angle BFC + \angle BEA = 270^{\circ}$. 上述结论中，所有正确结论的序号是( )

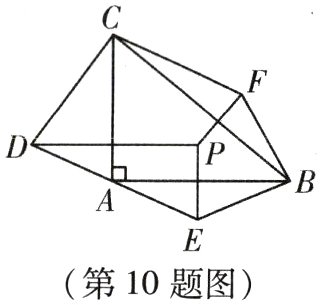
A. ①②
B. ①③
C. ②③
D. ①②③

答案： A

11. 已知直角三角形的两直角边长分别为$6\ cm$和$8\ cm$，则斜边上的高为________ $cm$.

答案： $\frac{24}{5}$

12. 关于$x$的不等式组$\begin{cases}x - b ＞ 2a \\ x - a ＜ 2b\end{cases}$的解集为$-3 ＜ x ＜ 3$，则$a$的值为________.

答案： -3

13. 如图所示，把一副直角三角尺$ACB$绕着$30^{\circ}$角的顶点$B$顺时针旋转，使得点$A$落在$CB$的延长线上的点$E$处，则$\angle BDC$的度数为________.

答案： $15^{\circ}$

14. 如图所示，直线$y = x + 1$(记为$l_1$)与直线$y = mx + n$(记为$l_2$)相交于点$P(a,2)$，则关于$x$的不等式$x + 1\geq mx + n$的解集为________.

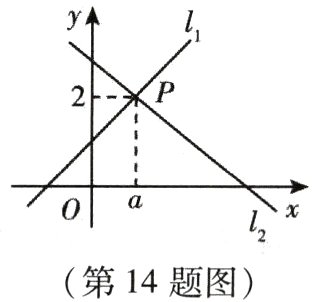
答案： $x\geqslant1$

15. 如图，在$Rt\triangle ABC$中，$\angle ABC = 90^{\circ}$，$AB = BC = \sqrt{2}$. 将$\triangle ABC$绕点$C$逆时针旋转$60^{\circ}$，得到$\triangle MNC$，连接$BM$，则$BM$的长是________.

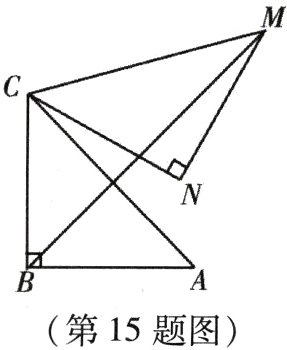
答案： $\sqrt{3}+1$

16. (本小题8分)解不等式(组)并将解集在数轴上表示出来.
(1)$4x + 5\geq6x - 3$； (2)$\begin{cases}x - 3(x - 2)\leq4 \\ \frac{1 + 2x}{3} ＞ x - 1\end{cases}$.

答案：
(1) 解：$x\leqslant4$ （数轴表示：在数轴上 -1 到 4 之间，4 处为实心点）
(2) 解：$1\leqslant x＜4$ （数轴表示：在数轴上 1 到 4 之间，1 处为实心点，4 处为空心点）

17. (本小题8分)已知关于$x$、$y$的方程组$\begin{cases}3x - y = 2a - 5 \\ x + 2y = 3a + 3\end{cases}$的解满足$0 ＜ x + y\leq3$.
(1)求$a$的取值范围；
(2)已知$a + b = 4$，且$z = 2a - 3b$，求$z$的最大值.

答案： 解：
(1) 由题$\begin{cases}x = a - 1\\y = a + 2\end{cases}$，
由$0 ＜ x + y\leqslant3$有$0 ＜ 2a + 1\leqslant3$得$-\frac{1}{2} ＜ a\leqslant1$.
(2) 由题$b = 4 - a$，则$z = 2a - 3(4 - a)=5a - 12$，
由$-\frac{1}{2} ＜ a\leqslant1$有$-\frac{29}{2} ＜ 5a - 12\leqslant -7$.
所以$z$的最大值为 -7.