《2025年学练考精品单元卷八年级数学全一册北师大版》

18. (本小题7分)已知：如图，$CE\perp AB$，$BF\perp AC$，$CE$与$BF$相交于点$D$，且$BD = CD$.
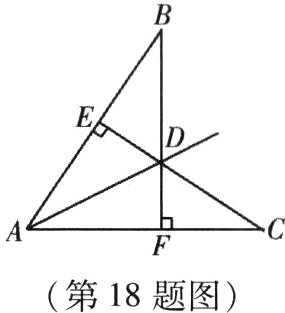
求证：点$D$在$\angle BAC$的平分线上.

答案： 证明：$\because CE\perp AB$，$BF\perp AC$，
$\therefore\angle BED=\angle CFD = 90^{\circ}$. 在$\triangle BDE$和$\triangle CDF$中，
$\because\angle BED=\angle CFD$，$\angle BDE=\angle CDF$，$BD = CD$，
$\therefore\triangle BDE\cong\triangle CDF(AAS)$，
$\therefore DE = DF$. 又$DE\perp AB$，$DF\perp AC$，
$\therefore$点$D$在$\angle BAC$的平分线上.

19. (本小题8分)如图所示，在等边$\triangle ABC$中，$D$是边$AC$上一点，连接$BD$. 将$\triangle BCD$绕点$B$逆时针旋转$60^{\circ}$得到$\triangle BAE$，连接$ED$. 若$BC = 10$，$BD = 9$，求$\triangle AED$的周长.

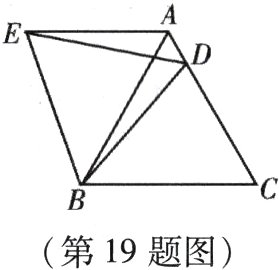
答案： 解：$\because\triangle BCD$绕点$B$逆时针旋转$60^{\circ}$得到$\triangle BAE$，
$\therefore CD = AE$，$BD = BE$.
$\because\triangle ABC$是等边三角形，$BC = 10$，$\therefore AC = BC = 10$.
$\therefore AE + AD = AC = 10$. 又$\angle DBE = 60^{\circ}$，
$\therefore\triangle DBE$是等边三角形，$\therefore DE = BD = 9$.
$\therefore\triangle AED$的周长为$DE + AE + AD = 9 + 10 = 19$.

20. (本小题8分)如图所示的直角坐标系中，$\triangle ABC$各顶点的坐标分别是$A(-2,-4)$，$B(0,-4)$，$C(1,-1)$.
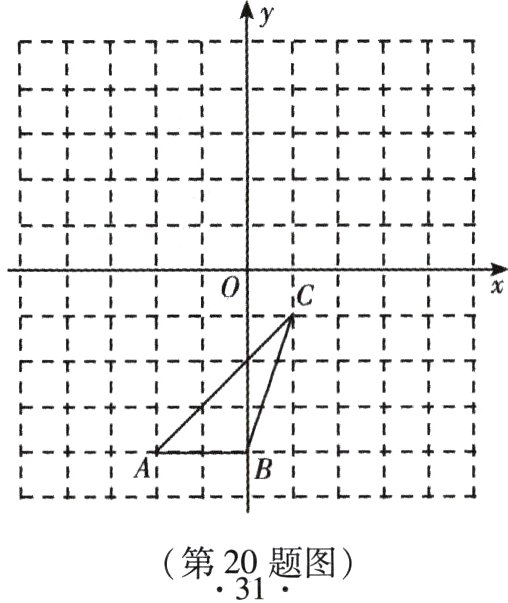
(1)在图中画出$\triangle ABC$向左平移3个单位后的$\triangle A_1B_1C_1$；
(2)在图中画出$\triangle ABC$绕原点$O$逆时针旋转$90^{\circ}$后的$\triangle A_2B_2C_2$.

答案：
解：
(1) 如图所示，$\triangle A_{1}B_{1}C_{1}$为所求的三角形.
(2) 如图所示，$\triangle A_{2}B_{2}C_{2}$为所求的三角形.