《2025年学练考精品单元卷八年级数学全一册北师大版》

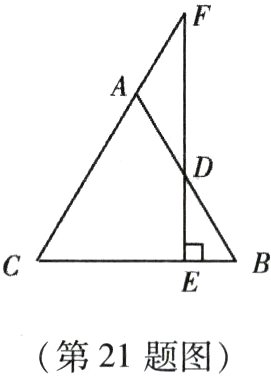
21. (本小题8分)已知:如图,$AB = AC$,$D$是$AB$上一点,$DE\perp BC$于点$E$,$ED$的延长线交$CA$的延长线于点$F$.求证:$\triangle ADF$是等腰三角形.

答案： 证明：
∵AB = AC，
∴∠B = ∠C.
∵FD⊥BC于点E，
∴∠FEB = ∠FEC = 90°.
∴∠B + ∠EDB = ∠C + ∠EFC = 90°，
∴∠EFC = ∠EDB.
∵∠EDB = ∠ADF，
∴∠EFC = ∠ADF，
∴△ADF是等腰三角形.

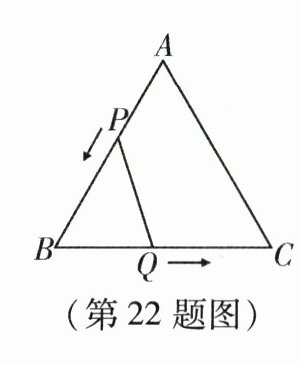
22. (本小题12分)如图,$\triangle ABC$是边长为3cm的等边三角形,动点$P$,$Q$同时从$A$,$B$两点出发,分别沿$AB$,$BC$的方向匀速移动,它们的速度都是1cm/s,当点$P$到达点$B$时,$P$,$Q$两点停止运动.设点$P$的运动时间为$t\ s$,则当$t$为何值时,$\triangle PBQ$是直角三角形？

答案： 解：根据题意，得AP = t cm，BQ = t cm.
在△ABC中，AB = BC = 3 cm，∠B = 60°，
∴BP = (3 - t)cm.
在△PBQ中，BP = (3 - t)cm，BQ = t cm，
若△PBQ是直角三角形，
则∠BQP = 90°或∠BPQ = 90°.
当∠BQP = 90°时，∠BPQ = 90° - ∠B = 30°，
∴BQ = $\frac{1}{2}$BP，即t = $\frac{1}{2}$(3 - t)，解得t = 1.
当∠BPQ = 90°时，∠BQP = 90° - ∠B = 30°，
∴BP = $\frac{1}{2}$BQ，即3 - t = $\frac{1}{2}$t，解得t = 2.
即当t为1或2时，△PBQ是直角三角形.

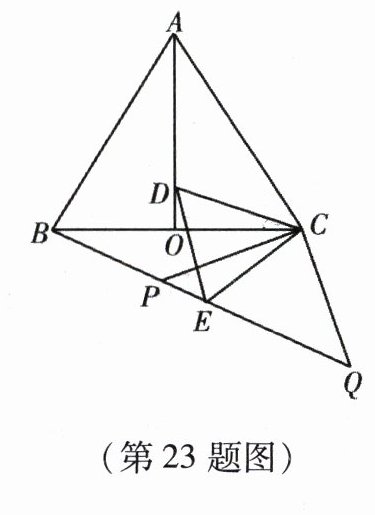
23. (本小题12分)如图,等边$\triangle ABC$中,$AO$是$\angle BAC$的角平分线,$D$为$AO$上一点,以$CD$为一边且在$CD$下方作等边$\triangle CDE$,连接$BE$.
(1)求证:$\triangle ACD\cong\triangle BCE$;
(2)延长$BE$至$Q$,$P$为$BQ$上一点,连接$CP$、$CQ$使$CP = CQ = 5$,若$BC = 8$时,求$PQ$的长.

答案：

(1) 证明：
∵△ABC与△DCE是等边三角形，
∴AC = BC，DC = EC，∠ACB = ∠DCE = 60°，
∴∠ACD + ∠DCB = ∠ECB + ∠DCB = 60°，
∴∠ACD = ∠BCE，
∴△ACD≌△BCE(SAS)；

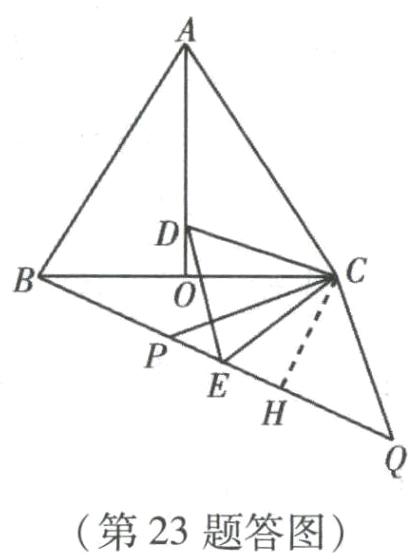
(2) 解：过点C作CH⊥BQ于H，
∵△ABC是等边三角形，AO是角平分线，
∴∠DAC = 30°，
∵△ACD≌△BCE，
∴∠PBC = ∠DAC = 30°，
∴在Rt△BHC中，CH = $\frac{1}{2}$BC = $\frac{1}{2}$×8 = 4，
∵PC = CQ = 5，CH = 4，
∴PH = QH = 3，
∴PQ = 6.