11. 因式分解:mn(n - m)-n(m - n)=________.
答案:
$n(n - m)(m + 1)$
12. 已知实数$x,y$满足$x^{2}+4x + y^{2}-6y + 13 = 0$,则$x + y$的值为________.
答案:
1
13. 若多项式$(3x + 2)(2x - 5)+(5 - 2x)(2x - 1)$可分解为$(2x + m)(x + n)$,其中$m,n$均为整数,则$mn$的值为________.
答案:
-15
14. 若$x + y = -1$,则$x^{4}+5x^{3}y + x^{2}y + 8x^{2}y^{2}+xy^{2}+5xy^{3}+y^{4}$的值等于________.
答案:
1
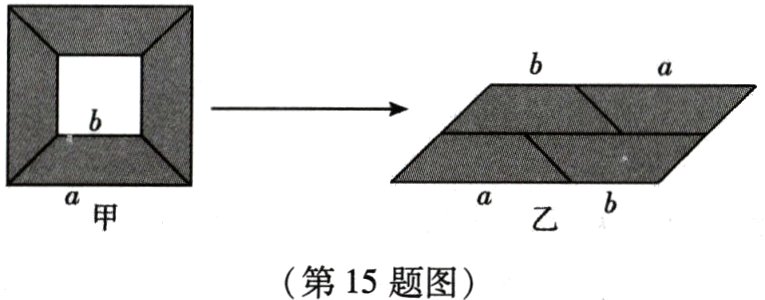
15. 从边长为$a$的正方形纸板中挖去一个边长为$b$的小正方形纸板后,将其裁成四个相同的等腰梯形,如图甲,然后拼成一个平行四边形,如图乙,那么通过计算两个图形阴影部分的面积,可以验证成立的等式为____________________.

答案:
$a^{2}-b^{2}=(a + b)(a - b)$
16. (本小题12分)因式分解:
(1)$2x^{2}y - 8xy + 8y$;
(2)$a^{2}(x - y)-9b^{2}(x - y)$;
(3)$9(m + 2n)^{2}-4(m - 2n)^{2}$;
(4)$(y^{2}-1)^{2}+6(1 - y^{2})+9$.
(1)$2x^{2}y - 8xy + 8y$;
(2)$a^{2}(x - y)-9b^{2}(x - y)$;
(3)$9(m + 2n)^{2}-4(m - 2n)^{2}$;
(4)$(y^{2}-1)^{2}+6(1 - y^{2})+9$.
答案:
解:
(1)原式$=2y(x - 2)^{2}$.
(2)原式$=(x - y)(a + 3b)(a - 3b)$.
(3)原式$=(m + 10n)(5m + 2n)$.
(4)原式$=(y + 2)^{2}(y - 2)^{2}$.
(1)原式$=2y(x - 2)^{2}$.
(2)原式$=(x - y)(a + 3b)(a - 3b)$.
(3)原式$=(m + 10n)(5m + 2n)$.
(4)原式$=(y + 2)^{2}(y - 2)^{2}$.
17. (本小题6分)已知$a + b = 2,ab = 2$,求$a^{2}b + ab^{2}$的值.
答案:
解:$\because a + b = 2$, $ab = 2$,
$\therefore a^{2}b+ab^{2}=ab(a + b)=2\times2 = 4$.
$\therefore a^{2}b+ab^{2}=ab(a + b)=2\times2 = 4$.
查看更多完整答案,请扫码查看


