《2025年学练考精品单元卷八年级数学全一册北师大版》

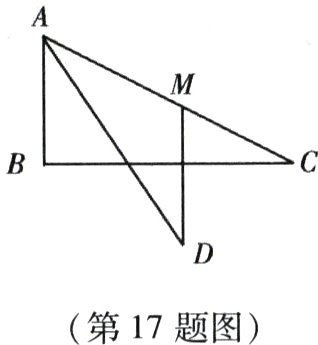
17. (本小题8分)如图,在$\triangle ABC$中,$\angle B = 90^{\circ}$,$M$是$AC$上任意一点($M$与$A$不重合),$MD\perp BC$,且交$\angle BAC$的平分线于点$D$,求证:$MA = MD$.

答案： 证明：
∵MD⊥BC，∠B = 90°，
∴AB//MD，
∴∠BAD = ∠D. 又
∵AD为∠BAC的平分线，
∴∠BAD = ∠MAD，
∴∠D = ∠MAD，
∴MA = MD.

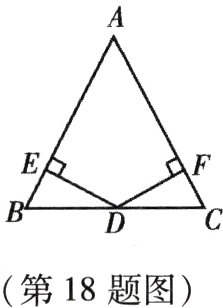
18. (本小题9分)如图,在$\triangle ABC$中,$AB = AC$,$D$为$BC$边的中点,过点$D$作$DE\perp AB$,$DF\perp AC$,垂足分别为$E$,$F$.
(1)求证:$\triangle BED\cong\triangle CFD$;
(2)若$\angle A = 60^{\circ}$,$BE = 1$,求$\triangle ABC$的周长.

答案：
(1) 证明：
∵AB = AC，
∴∠B = ∠C.
∵DE⊥AB，DF⊥AC，
∴∠DEB = ∠DFC = 90°.
∵D是BC的中点，
∴BD = CD.
∴△BED≌△CFD(AAS).
(2) 解：
∵AB = AC，∠A = 60°，
∴△ABC是等边三角形，
∴AB = BC = CA，∠B = 60°.
又
∵DE⊥AB，
∴∠EDB = 30°，
∴BD = 2BE = 2，
∴BC = 2BD = 4，
∴△ABC的周长为AB + BC + CA = 3BC = 12.

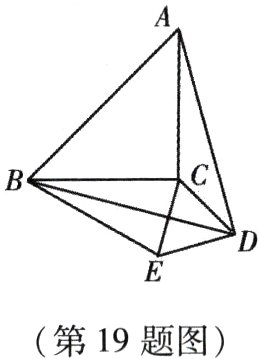
19. (本小题8分)如图所示,以等腰直角三角形$ABC$的斜边$AB$为边作等边$\triangle ABD$,连接$DC$,以$DC$为边作等边$\triangle DCE$,$B$,$E$在$C$,$D$的同侧,若$AB = \sqrt{2}$,求$BE$的长.

答案： 解：
∵△ABD和△CDE都是等边三角形，
∴AD = BD，CD = DE，∠ADB = ∠CDE = 60°.
∴∠ADB - ∠CDB = ∠CDE - ∠CDB，
即∠ADC = ∠BDE. 在△ADC和△BDE中，
∵AD = BD，CD = DE，∠ADC = ∠BDE，
∴△ADC≌△BDE(SAS)，
∴AC = BE. 又AC = BC，
∴BE = BC. 在等腰直角△ABC中，AB = $\sqrt{2}$，
∴AC = BC = 1，故BE = 1.

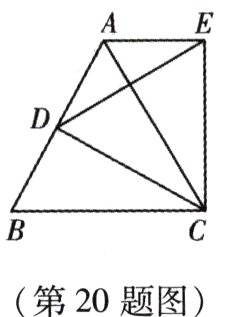
20. (本小题10分)如图,在等边三角形$ABC$中,$D$是$AB$边上的动点,以$CD$为一边,向上作等边三角形$EDC$,连接$AE$.
(1)$\triangle DBC$和$\triangle EAC$全等吗？请说出你的理由;
(2)试说明$AE// BC$.

答案： 解：
(1) △DBC和△EAC全等. 理由：
∵△ABC和△EDC都是等边三角形，
∴∠ACB = 60°，∠DCE = 60°，AC = BC，DC = EC，
∴∠BCD = 60° - ∠ACD，∠ACE = 60° - ∠ACD，
∴∠BCD = ∠ACE. 在△DBC和△EAC中，
∵BC = AC，∠BCD = ∠ACE，DC = EC，
∴△DBC≌△EAC(SAS).
(2)
∵△DBC≌△EAC，
∴∠EAC = ∠B = 60°.
又
∵∠ACB = 60°，
∴∠EAC = ∠ACB，
∴AE//BC.