《2025年学练考精品单元卷八年级数学全一册北师大版》

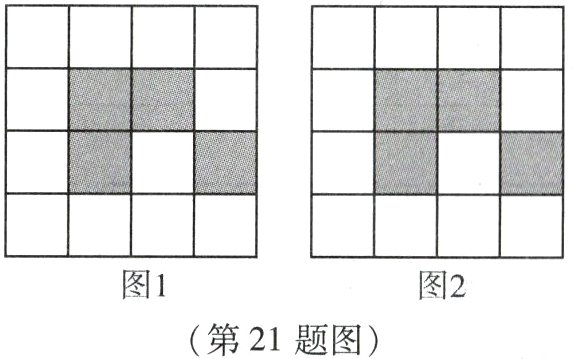
21. (本小题10分)如图,4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.

答案：
解：
(1)如图所示：

(2)如图所示：

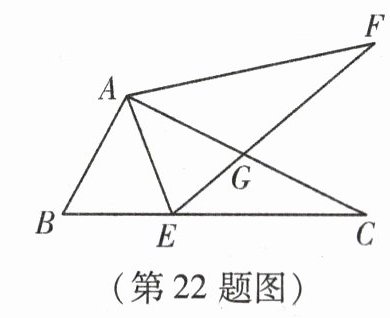
22. (本小题12分)如图,在△ABC中,点E在BC边上,AE = AB,将线段AC绕A点旋转到AF的位置,使得∠CAF = ∠BAE,连接EF,EF与AC交于点G.
(1)求证:BC = EF;
(2)若∠ABC = 64°,∠ACB = 25°,求∠AGE的度数.

答案：
(1)证明：$\because \angle CAF = \angle BAE$，$\therefore \angle BAC = \angle EAF$.
$\because$将线段$AC$绕$A$点旋转到$AF$的位置，
$\therefore AC = AF$.
在$\triangle ABC$与$\triangle AEF$中，$\begin{cases}AB = AE\\\angle BAC = \angle EAF\\AC = AF\end{cases}$
$\therefore \triangle ABC\cong \triangle AEF(SAS)$，$\therefore BC = EF$；
(2)解：$\because AB = AE$，$\angle ABC = 64^{\circ}$，
$\therefore \angle BAE = 180^{\circ} - 64^{\circ} \times 2 = 52^{\circ}$，
$\therefore \angle FAG = \angle BAE = 52^{\circ}$. $\because \triangle ABC\cong \triangle AEF$，
$\therefore \angle F = \angle C = 25^{\circ}$，
$\therefore \angle FGC = \angle FAG + \angle F = 52^{\circ} + 25^{\circ} = 77^{\circ}$，
$\therefore \angle AGE = 77^{\circ}$.

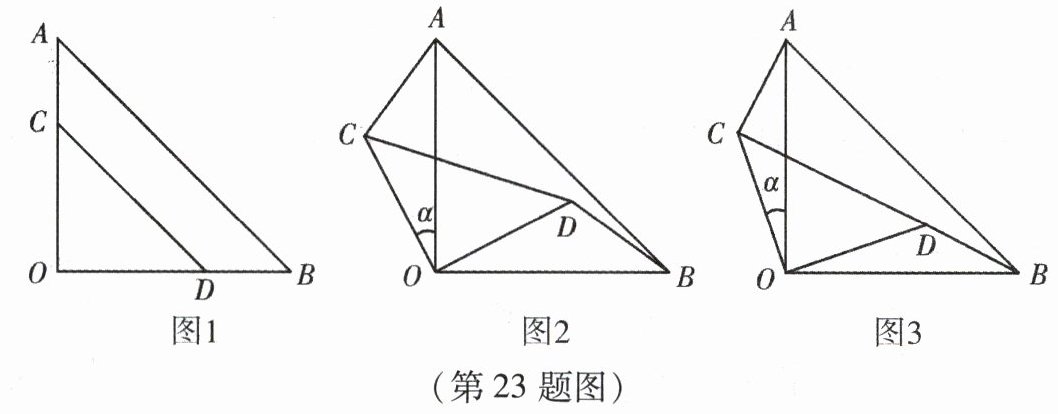
23. (本小题12分)两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB = 25.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°＜α＜90°)角度,如图2所示.
(1)在图2中,求证:AC = BD,且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,若AC = 7,求CD的长.

答案：
证明：如图2中，延长$BD$交$OA$于点$G$，交$AC$于点$E$.

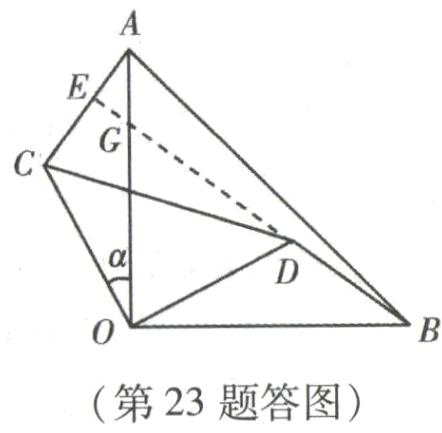
$\because \angle AOB = \angle COD = 90^{\circ}$，$\therefore \angle AOC = \angle DOB$，
在$\triangle AOC$和$\triangle BOD$中，$\begin{cases}OA = OB\\\angle AOC = \angle BOD\\OC = OD\end{cases}$
$\therefore \triangle AOC\cong \triangle BOD$，$\therefore AC = BD$，$\angle CAO = \angle DBO$.
$\because \angle DBO + \angle OGB = 90^{\circ}$，$\therefore \angle OGB = \angle AGE$，
$\therefore \angle CAO + \angle AGE = 90^{\circ}$，$\therefore \angle AEG = 90^{\circ}$，$\therefore AC \perp BD$.
(2)解：由
(1)可知$AC = BD$，$AC \perp BD$.
$\because BD$，$CD$在同一直线上，
$\therefore \triangle ABC$是直角三角形.
由勾股定理得$BC = \sqrt{AB^{2} - AC^{2}} = \sqrt{25^{2} - 7^{2}} = 24$，
$\therefore CD = BC - BD = BC - AC = 17$.