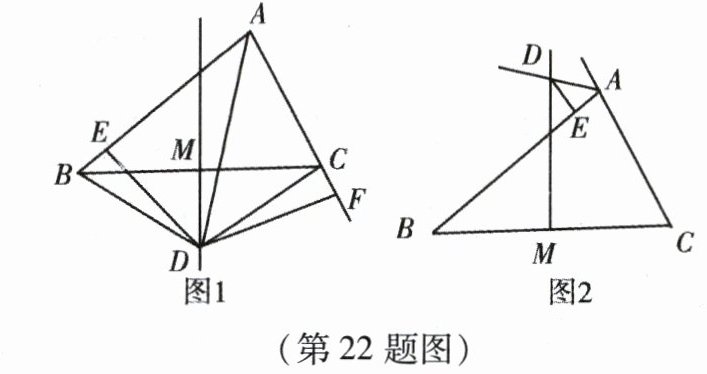
22. (本小题12分)如图1,△ABC的边BC的中垂线DM交∠BAC的平分线AD于D,DE⊥AB于点E,DF⊥AC于F. 连接DB、DC.
(1)求证:△DBE≌△DFC;
(2)求证:AB + AC = 2AE;
(3)如图2,若△ABC的边BC的中垂线DM交∠BAC的外角平分线AD于D,DE⊥AB于点E,且AB>AC,写出AE、BE、AC之间的等量关系.(不需证明,只需在图2中作出辅助线,说明证哪两个三角形全等即可)
(1)求证:△DBE≌△DFC;
(2)求证:AB + AC = 2AE;
(3)如图2,若△ABC的边BC的中垂线DM交∠BAC的外角平分线AD于D,DE⊥AB于点E,且AB>AC,写出AE、BE、AC之间的等量关系.(不需证明,只需在图2中作出辅助线,说明证哪两个三角形全等即可)

答案:
(1) 证明:$\because DM\perp$平分$BC$,$\therefore DB = DC$,$\because\angle 1=\angle 2$. $DE\perp AB$,$DF\perp AC$,$\therefore DE = DF$,$\therefore Rt\triangle DEB\cong Rt\triangle DFC(HL)$.
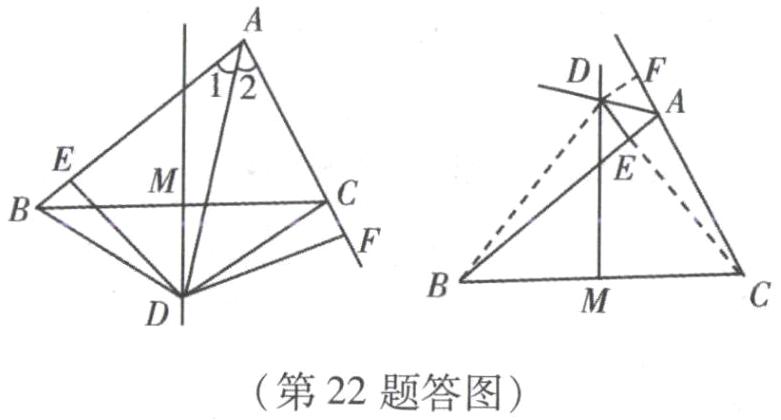
(2) 证明:$\because DE = DF$,$AD = AD$,$\angle AED=\angle AFD = 90^{\circ}$,$\therefore Rt\triangle ADE\cong Rt\triangle ADF(HL)$,$\therefore AE = AF$. 又$\because Rt\triangle DEB\cong Rt\triangle DFC$,$\therefore BE = CF$,$AB + AC = AE + BE + AF - CF = 2AE$.
(3) 解:$BE = AE + AC$. 作$DF\perp AC$于$F$,连接$DB$、$DC$,证明$Rt\triangle DEB\cong Rt\triangle DFC$,$Rt\triangle ADE\cong Rt\triangle ADF$即可.
(1) 证明:$\because DM\perp$平分$BC$,$\therefore DB = DC$,$\because\angle 1=\angle 2$. $DE\perp AB$,$DF\perp AC$,$\therefore DE = DF$,$\therefore Rt\triangle DEB\cong Rt\triangle DFC(HL)$.

(2) 证明:$\because DE = DF$,$AD = AD$,$\angle AED=\angle AFD = 90^{\circ}$,$\therefore Rt\triangle ADE\cong Rt\triangle ADF(HL)$,$\therefore AE = AF$. 又$\because Rt\triangle DEB\cong Rt\triangle DFC$,$\therefore BE = CF$,$AB + AC = AE + BE + AF - CF = 2AE$.
(3) 解:$BE = AE + AC$. 作$DF\perp AC$于$F$,连接$DB$、$DC$,证明$Rt\triangle DEB\cong Rt\triangle DFC$,$Rt\triangle ADE\cong Rt\triangle ADF$即可.
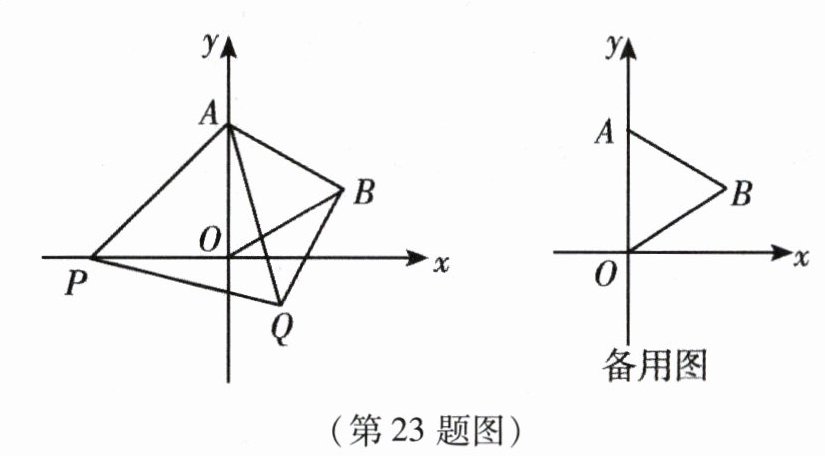
23. (本小题12分)如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形△APQ.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ//AB时,求P点的坐标.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ//AB时,求P点的坐标.

答案:
解:
(1) 作$BM\perp y$轴于$M$,$\because OA = OB = AB = 2$,$\therefore OM = 1$,$BM=\sqrt{3}$,$\therefore B(\sqrt{3},1)$.
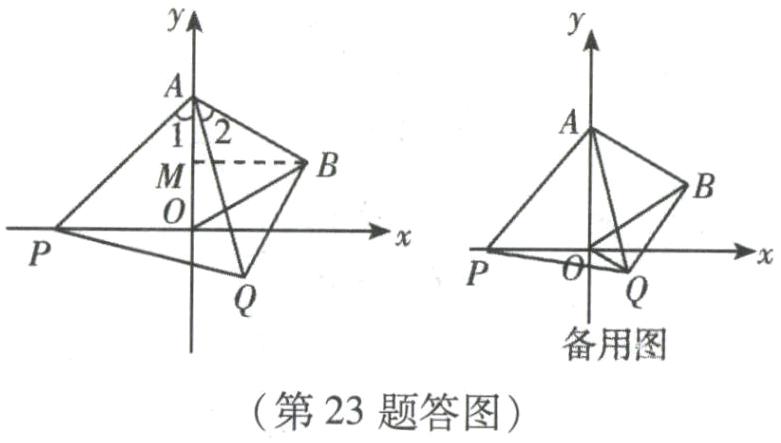
(2)$\because AP = AQ$,$AO = AB$,$\angle 1=\angle 2 = 60^{\circ}-\angle OAQ$,$\therefore\triangle APO\cong\triangle AQB(SAS)$,$\therefore\angle AOP=\angle ABQ = 90^{\circ}$,即$\angle ABQ$的大小不变.
(3) 当$OQ// AB$时,$\angle BQO = 90^{\circ}$,$\because\angle OBQ = 90^{\circ}-60^{\circ}=30^{\circ}$,$OB = 2$,$\therefore OQ = 1$,$BQ=\sqrt{3}$. $\because\triangle APO\cong\triangle AQB$,$\therefore PO = BQ=\sqrt{3}$,$\therefore P(-\sqrt{3},0)$.
解:
(1) 作$BM\perp y$轴于$M$,$\because OA = OB = AB = 2$,$\therefore OM = 1$,$BM=\sqrt{3}$,$\therefore B(\sqrt{3},1)$.

(2)$\because AP = AQ$,$AO = AB$,$\angle 1=\angle 2 = 60^{\circ}-\angle OAQ$,$\therefore\triangle APO\cong\triangle AQB(SAS)$,$\therefore\angle AOP=\angle ABQ = 90^{\circ}$,即$\angle ABQ$的大小不变.
(3) 当$OQ// AB$时,$\angle BQO = 90^{\circ}$,$\because\angle OBQ = 90^{\circ}-60^{\circ}=30^{\circ}$,$OB = 2$,$\therefore OQ = 1$,$BQ=\sqrt{3}$. $\because\triangle APO\cong\triangle AQB$,$\therefore PO = BQ=\sqrt{3}$,$\therefore P(-\sqrt{3},0)$.
查看更多完整答案,请扫码查看


