《2025年学练考精品单元卷八年级数学全一册北师大版》

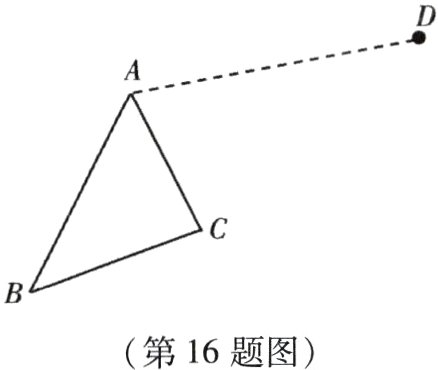
16. (本小题7分)如图,经过平移,△ABC的顶点移到了点D,作出平移后的△DEF.

答案：
解：如图，$\triangle DEF$即为所求.

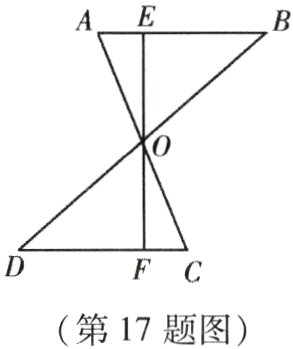
17. (本小题8分)如图,AC与BD互相平分且相交于点O,点E、F分别在AB、CD上,且AE = CF,试利用“中心对称”的有关知识,证明点E、O、F在同一直线上且OE = OF.

答案：
证明：如图，连接 $AD$、$BC$，

$\because AC$与 $BD$互相平分且相交于点 $O$，
$\therefore$四边形 $ABCD$是平行四边形，
$\therefore$点 $O$是平行四边形 $ABCD$的对称中心.
$\because AE = CF$，$\therefore$点 $E$、$F$是对称点，
$\therefore$点 $E$、$O$、$F$在同一直线上且 $OE = OF$.

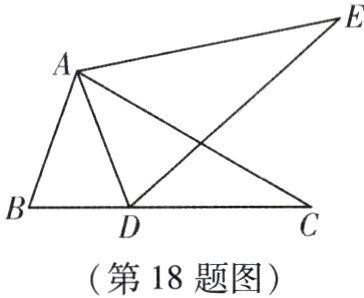
18. (本小题8分)如图,将△ABC绕点A逆时针旋转得到△ADE,点D在BC上,已知∠BAD = 40°,求∠ADE的大小.

答案： 解：$\because$把$\triangle ABC$绕点 $A$逆时针旋转得到$\triangle ADE$，
$\therefore AB = AD$，$\angle ABC = \angle ADE$，$\because \angle BAD = 40^{\circ}$，
$\therefore \angle ABC = \angle ADB = \angle ADE = \frac{1}{2}(180^{\circ} - \angle BAD)$
$= 70^{\circ}$.

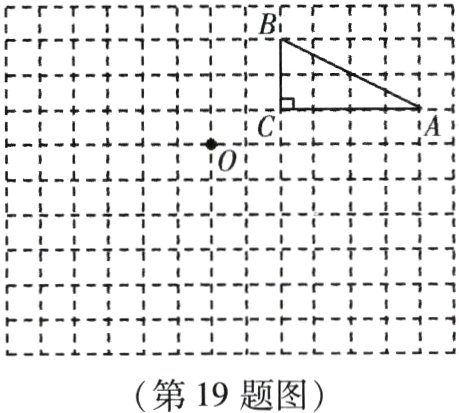
19. (本小题10分)如图,在由边长为1个单位长度的小正方形组成的网格中,点A、B、C都是格点.
(1)将△ABC向左平移6个单位长度得到△A₁B₁C₁,请画出△A₁B₁C₁;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A₂B₂C₂,请画出△A₂B₂C₂.

答案：
解：
(1)如图所示：$\triangle A_{1}B_{1}C_{1}$，即为所求.
(2)如图所示：$\triangle A_{2}B_{2}C_{2}$即为所求.

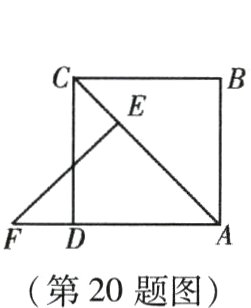
20. (本小题10分)如图,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置.
(1)指出它的旋转中心;
(2)说出它的旋转方向和旋转角是多少度;
(3)分别写出点A,B,C的对应点.

答案： 解：
(1)它的旋转中心为点 $A$.
(2)它的旋转方向为逆时针方向，旋转角是45度.
(3)点 $A$，$B$，$C$的对应点分别为点 $A$，$E$，$F$.