《2025年学练考精品单元卷八年级数学全一册北师大版》

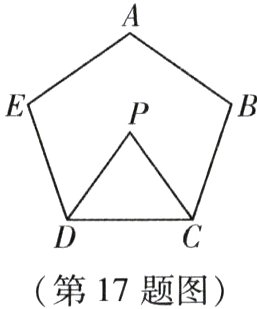
17.(本小题8分)如图,在五边形ABCDE中,∠A + ∠B + ∠E = 300°,DP,CP分别平分∠EDC,∠BCD,求∠P的度数.

答案： 解:
∵五边形的内角和等于540°，
∠A+∠B+∠E=300°,
∴∠BCD+∠CDE=240°;
∵DP,CP分别平分∠EDC,∠BCD,
∴∠PCD+∠CDP=$\frac{240°}{2}$=120°,
∴∠P=180°−(∠PCD+∠CDP)
=180°−120°=60°.

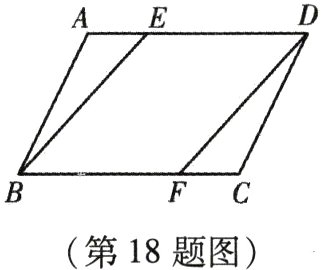
18.(本小题10分)如图,在平行四边形ABCD中,E,F分别在AD,BC边上,且AE = CF.
求证:(1)△ABE≌△CDF;(2)四边形BFDE是平行四边形.

答案： 解:
(1)
∵四边形ABCD是平行四边形，
∴AB=CD,∠A=∠C,又
∵AE=CF,
∴△ABE≌△CDF;
(2)
∵四边形ABCD是平行四边形，
∴AD//BC,AD=BC,又
∵AE=CF,
∴AD−AE=BC−CF,即DE=BF,
又
∵DE//BF,
∴四边形BFDE是平行四边形.

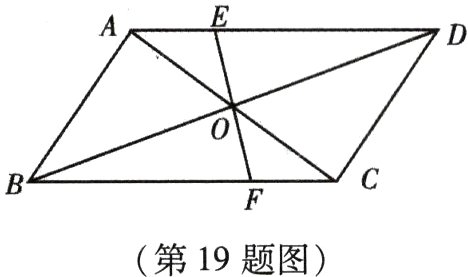
19.(本小题8分)已知:如图,在▱ABCD中,对角线AC,BD相交于点O,EF过点O分别交AD,BC 于点E,F.求证:OE = OF.

答案： 证明:
∵四边形ABCD是平行四边形，
∴AD//BC,OA=OC,
∴∠EAO=∠FCO,∠AEO=∠CFO,
∴△AOE≌△COF,故OE=OF.

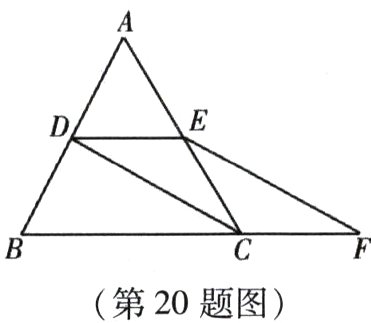
20.(本小题10分)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF = $\frac{1}{2}$BC,连接CD和EF:
(1)求证:DE = CF;
(2)求EF的长.

答案：
(1)证明:
∵D,E分别为AB,AC的中点，
∴DE为△ABC的中位线，
∴DE$\underline{\underline{//}}$$\frac{1}{2}$BC,
∵延长BC至点F,使CF=$\frac{1}{2}$BC,
∴DE=FC.
(2)解:
∵DE$\underline{\underline{//}}$FC,
∴四边形DEFC是平行四边形，
∴DC=EF,
∵D为AB的中点，
等边△ABC的边长是2，
∴AD=BD=1,CD⊥AB,BC=2,
∴DC=EF=$\sqrt{3}$;