《2025年学练考精品单元卷八年级数学全一册北师大版》

17. (本小题8分)分解因式：
(1)$3a^{2}-6ab + 3b^{2}$；
(2)$(x - y)a^{2}+(y - x)b^{2}$.

答案： 解：
(1) $3a^{2}-6ab + 3b^{2}$
$=3(a^{2}-2ab + b^{2})$
$=3(a - b)^{2}$；
(2) $(x - y)a^{2}+(y - x)b^{2}$
$=(x - y)a^{2}-(x - y)b^{2}$
$=(x - y)(a^{2}-b^{2})$
$=(x - y)(a + b)(a - b)$.

18. (本小题8分)先化简，再求值：$(1+\frac{1}{x - 2})\div\frac{x^{2}-2x + 1}{x^{2}-4}$，其中$x = - 5$.

答案： 解：原式 $=(\frac{x - 2}{x - 2}+\frac{1}{x - 2})\div\frac{(x - 1)^{2}}{(x + 2)(x - 2)}=\frac{x - 1}{x - 2}\cdot\frac{(x + 2)(x - 2)}{(x - 1)^{2}}=\frac{x + 2}{x - 1}$，把 $x = -5$ 代入计算，原式 $=\frac{-5 + 2}{-5 - 1}=\frac{1}{2}$.

19. (本小题8分)已知关于$x$的方程$\frac{3x - 1}{x + 1}-\frac{m}{x + 1}=1$.
(1)在解该方程时，去分母后所得整式方程的解不是原分式方程的解，求$m$的值；
(2)若该方程的解为负数，求$m$的取值范围.

答案： 解：
(1) 方程两边同乘 $(x + 1)$ 得：$3x - 1 - m = x + 1$，移项、合并同类项得：$2x = 2 + m$，
系数化为 1 得：$x=\frac{2 + m}{2}$，
∵去分母后所得整式方程的解不是原分式方程的解，
∴当 $x = -1$ 时，满足题意，
∴$\frac{2 + m}{2}=-1$，解得：$m = -4$；
(2) 方程两边同乘 $(x + 1)$ 得：$3x - 1 - m = x + 1$，
移项、合并同类项得：$2x = 2 + m$，
系数化为 1 得：$x=\frac{2 + m}{2}$，
∵该方程的解为负数，
∴$\frac{2 + m}{2}＜0$，解得：$m ＜ -2$，
由
(1)可得，要使原分式方程有解，则 $m\neq -4$，
∴$m$ 的取值范围为：$m ＜ -2$ 且 $m\neq -4$.

20. (本小题9分)运用分式方程，解决下面问题：
为改善城市排水系统，某市需要新铺设一段全长为3000 m的排水管道. 为了减少施工对城市交通的影响，实际施工时每天的工效是原计划的1.2倍，结果提前5天完成这一任务.
(1)这个工程队原计划每天铺设管道多少米？
(2)填空：在这项工程中，如果要求工程队提前6天完成任务，那么实际施工时每天的工效比原计划增加______(填百分数，不写过程).

答案： 解：
(1) 设这个工程队原计划每天铺设管道 $x$ m，
根据题意，得 $\frac{3000}{x}-\frac{3000}{1.2x}=5$，解得 $x = 100$，
经检验，$x = 100$ 是原方程的解.
答：这个工程队原计划每天铺设管道 100 m.
(2) 25%

21. (本小题12分)如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，$Rt\triangle ABC$的顶点均在格点上.
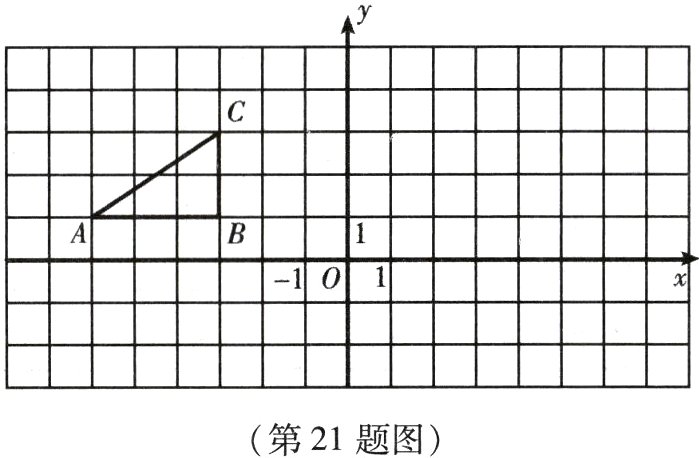
(1)将$Rt\triangle ABC$沿$x$轴正方向平移8个单位得到$Rt\triangle A_{1}B_{1}C_{1}$，试在图上画出$Rt\triangle A_{1}B_{1}C_{1}$的图形，并写出点$A_{1}$的坐标(______，______)；
(2)若$Rt\triangle ABC$内部一点$P$的坐标为$(a,b)$，则平移后点$P$的对应点$P_{1}$的坐标是(______，______)；
(3)将原来的$Rt\triangle ABC$绕着点$O$顺时针旋转180°得到$Rt\triangle A_{2}B_{2}C_{2}$，试在图上画出$Rt\triangle A_{2}B_{2}C_{2}$的图形.

答案：
解：
(1) $Rt\triangle A_{1}B_{1}C_{1}$ 如图所示，$A_{1}(2,1)$.
(2) $P_{1}(a + 8,b)$.
(3) $Rt\triangle A_{2}B_{2}C_{2}$ 如图所示.