《2025年学练考精品单元卷八年级数学全一册北师大版》

22. (本小题10分)某老师五一将带领该校市级“三好学生”去北京旅游，甲旅行社说：“如果老师买全票一张，则其余的学生可享受半价优惠. ”乙旅行社说：“包括老师在内全部按票价的六折优惠. ”若全票价为2400元，两家旅行社的服务质量相同，根据“三好学生”的人数你认为选择哪一家旅行社才比较合算？

答案： 解：设三好学生为 $x$ 人，选择甲旅行社费用为 $y_{1}$ 元，乙旅行社费用为 $y_{2}$ 元，由题意，得 $y_{1}=2400\times0.5x + 2400$，$y_{1}=1200x + 2400$. $y_{2}=0.6\times2400(x + 1)=1440x + 1440$. 当 $y_{1}＞y_{2}$ 时，$1200x + 2400＞1440x + 1440$，解得：$x ＜ 4$；当 $y_{1}=y_{2}$ 时，$1200x + 2400=1440x + 1440$，解得：$x = 4$；当 $y_{1}＜y_{2}$ 时，$1200x + 2400＜1440x + 1440$，解得：$x ＞ 4$. 综上所述，当三好学生人数少于 4 人时，选择乙旅行社合算；等于 4 人时，甲、乙两家一样合算；多于 4 人时，选择甲旅行社合算.

23. (本小题12分)如图，已知$\triangle BAD$和$\triangle BCE$均为等腰直角三角形，$\angle BAD=\angle BCE = 90^{\circ}$，点$M$为$DE$的中点. 过点$E$与$AD$平行的直线交射线$AM$于点$N$.
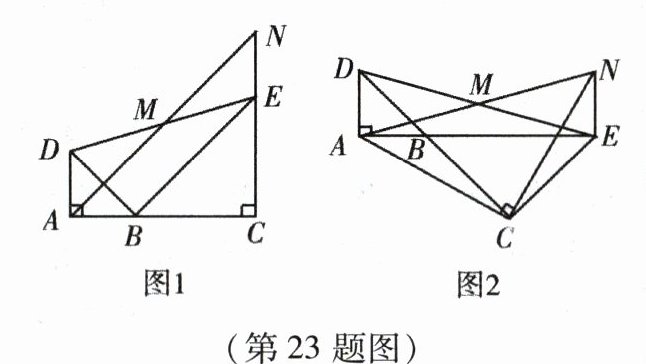
(1)当$A$，$B$，$C$三点在同一直线上时(如图1)，求证：$M$为$AN$的中点；
(2)将图1中$\triangle BCE$绕点$B$旋转，当$A$，$B$，$E$三点在同一直线上时(如图2)，求证：$\triangle CAN$为等腰直角三角形；
(3)在(2)条件下，已知$AD = 1$，$CE=\sqrt{2}$，试求$AN$的长.

答案： 解：
(1)
∵点 $M$ 为 $DE$ 的中点，
∴ $DM = ME$.
∵ $AD// EN$，
∴ $\angle ADM=\angle NEM$，
又
∵ $\angle DMA=\angle EMN$，
∴ $\triangle DMA\cong\triangle EMN$，
∴ $AM = MN$，即 $M$ 为 $AN$ 的中点.
(2) 由
(1)中 $\triangle DMA\cong\triangle EMN$ 可知 $DA = EN$，
又
∵ $DA = AB$，
∴ $AB = NE$.
∵ $\angle ABC=\angle NEC = 135^{\circ}$，$BC = CE$，
∴ $\triangle ABC\cong\triangle NEC$，
∴ $AC = CN$，$\angle ACB=\angle NCE$.
∵ $\angle BCE=\angle BCN+\angle NCE = 90^{\circ}$，
∴ $\angle BCN+\angle ACB = 90^{\circ}$，
∴ $\angle ACN = 90^{\circ}$，
∴ $\triangle CAN$ 为等腰直角三角形.
(3) 由
(2)知，$NE = AD = 1$，在等腰直角三角形 $BAD$ 中，$AD = 1$，
∴ $AB = AD = 1$，
在等腰直角三角形 $BCE$ 中，$CE=\sqrt{2}$，
∴ $BE = 2$，
∴ $AE = AB + BE = 3$
由
(2)知，$\angle AEN = 90^{\circ}$，
在 $Rt\triangle AEN$ 中，$AE = 3$，$NE = 1$，
根据勾股定理得，$AN=\sqrt{10}$.