《2025年学练考精品单元卷八年级数学全一册北师大版》

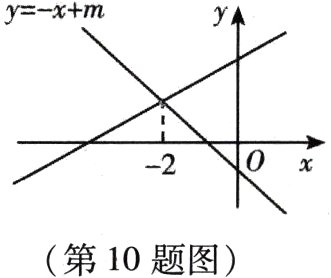
10. 如图,直线$y = - x + m$与$y = x + 3$的交点的横坐标为$-2$,则关于$x$的不等式$- x + m ＞ x + 3 ＞ 0$的取值范围为(　　　)
A. $x ＞ - 2$　　　　　　　　　　　　　　　　　　B. $x ＜ - 2$
C. $-3 ＜ x ＜ - 2$　　　　　　　　　　　　　　　D. $-3 ＜ x ＜ - 1$
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案： C

11. 用不等式表示：$x$与5的差不小于$x$的2倍：____________________.

答案： $x - 5\geq2x$

12. 已知点$P(m - 3,m + 1)$在第一象限,则$m$的取值范围是________.

答案： $m ＞ 3$

13. 若关于$x$的不等式组$\begin{cases}\frac{x + 1}{2} ＜ 3 + x \\x ＜ m\end{cases}$的所有整数解的和是$-7$,则$m$的取值范围是____________.

答案： $2 ＜ m\leq3$ 或 $-3 ＜ m\leq -2$

14. 把43个苹果分给若干个学生,除一名学生分得的苹果不足3个外,其余每人均分得6个苹果,求学生的人数.若设学生有$x$人,则可以列出不等式组为____________________.

答案： $\begin{cases}43 - 6(x - 1) ＜ 3 \\ 43 - 6(x - 1)\geq0\end{cases}$

15. 已知不等式$- x + 5 ＞ 3x - 3$的解集是$x ＜ 2$,则直线$y = - x + 5$与$y = 3x - 3$的交点坐标是________.

答案： $(2,3)$

16. (本小题12分)解下列不等式(组),并把它们的解集在数轴上表示出来：
(1)$5(x - 1)\leqslant3(x + 1)$;
(2)$\frac{2x - 1}{2}-\frac{5x - 1}{4} ＜ 0$;
(3)$\begin{cases}x - 5 ＜ - 3 ①\\2x ＜ - 2 ②\end{cases}$;
(4)$\begin{cases}\frac{2x - 1}{3}-\frac{5x + 1}{2}\leqslant1 ①\\5x - 1 ＜ 3(x + 1) ②\end{cases}$.

答案： 解：
(1) $x\leq4$；
(2) $x ＞ -1$；
(3) $x ＜ -1$；
(4) $-1\leq x ＜ 2$。

17. (本小题7分)小明用100元钱去购买笔记本和钢笔共30件,已知每本笔记本2元,每支钢笔5元.那么小明最多能买多少支钢笔?

答案： 解：设购买 $x$ 支钢笔，则笔记本有 $(30 - x)$ 本，列方程为：$5x + 2(30 - x)\leq100$，解得 $3x\leq40$，$x\leq\frac{40}{3}$，答：最多能买 13 支钢笔。