《2025年单元双测全优测评卷八年级数学下册沪科版》

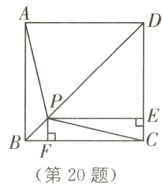
20. 如图,P为正方形ABCD对角线BD上一点，PE⊥CD于点E，PF⊥BC于点F.
　　(1)求证:PA=PC;
　　(2)若正方形ABCD的边长为1,求四边形PFCE的周长.
　　　　　　　　　　　　　　　　　　　　　　

答案： （1）
∵四边形ABCD是正方形，
∴AB = CB，∠ABD = ∠CBD = 45°.
在△ABP和△CBP中，$\begin{cases}AB = CB,\\\angle ABP=\angle CBP,\\BP = BP,\end{cases}$
∴△ABP≌△CBP.
∴PA = PC.
（2）
∵PE⊥CD，PF⊥BC，
∴∠PFC = 90°，∠PEC = 90°.
又∠BCD = 90°，
∴四边形PFCE是矩形.
∴EC = PF，PE = CF.
∵∠CBD = 45°，∠PFB = 90°，
∴BF = PF.
又BC = 1，
∴矩形PFCE的周长为2（PF + FC）= 2（BF + FC）= 2BC = 2.

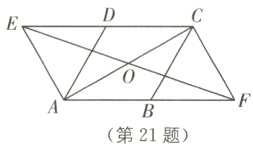
21. 如图,在□ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
　　(1)求证:四边形AFCE是平行四边形.
　　(2)若去掉已知条件的“∠DAB=60°”，上述的结论还成立吗？若成立，请写出证明过程;若不成立，请说明理由.
　　　　　　　　　　　　　　　　　　

答案： （1）
∵四边形ABCD是平行四边形，
∴DC//AB，∠DCB = ∠DAB = 60°.
∴∠ADE = ∠CBF = 60°.
∵AE = AD，CF = CB，
∴△AED，△CFB是等边三角形.
在□ABCD中，AD = BC，DC = AB，
∴ED = BF，ED + DC = BF + AB，
即EC = AF.
又DC//AB，即EC//AF，
∴四边形AFCE是平行四边形.
（2）上述结论还成立.证明如下：
∵四边形ABCD是平行四边形，
∴AD//BC，DC//AB，∠DCB = ∠DAB，AD = BC，DC = AB.
∴∠ADE = ∠DCB = ∠DAB = ∠CBF.
∵AE = AD，CF = CB，
∴∠AED = ∠ADE，∠CFB = ∠CBF.
∴∠AED = ∠CFB.
又AD = BC，
∴△ADE≌△CBF.
∴ED = FB.
∵DC = AB，
∴ED + DC = FB + AB，即EC = FA.
又DC//AB，即EC//AF.
∴四边形AFCE是平行四边形.

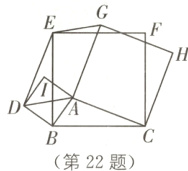
22. 如图，以△ABC的各边为边长，在边BC的同侧分别作正方形ABDI,正方形BCFE,正方形ACHG,连接AD,DE,EG.
　　(1)求证:△BDE≌△BAC.
　　(2)①设∠BAC=α,请用含α的代数式表示∠EDA,∠DAG.
②求证:四边形ADEG是平行四边形.
　　(3)当△ABC满足什么条件时，四边形ADEG是正方形？请说明理由.
　　

答案： （1）
∵四边形ABDI，四边形BCFE，四边形ACHG都是正方形，
∴AC = AG，AB = BD，BC = BE，∠GAC = ∠EBC = ∠DBA = 90°.
∴∠ABC = ∠EBD.
在△BDE和△BAC中，$\begin{cases}BD = BA,\\\angle DBE=\angle ABC,\\BE = BC,\end{cases}$
∴△BDE≌△BAC.
（2）①
∵△BDE≌△BAC，∠ADB = ∠BAD = 45°，∠BAC = α，
∴∠EDA = α - 45°，∠DAG = 360° - 45° - 90° - α = 225° - α.
②
∵△BDE≌△BAC，
∴DE = AC = AG，∠BAC = ∠BDE.
∵AD是正方形ABDI的对角线，
∴∠BDA = ∠BAD = 45°.
∵∠EDA = ∠BDE - ∠BDA = ∠BDE - 45°，由①，知∠DAG = 225° - ∠BAC.
∴∠EDA+∠DAG = ∠BDE - 45°+225° - ∠BAC = 180°.
∴DE//AG.
∴四边形ADEG是平行四边形.
（3）当△ABC满足∠BAC = 135°，且AC = $\sqrt{2}AB$时，四边形ADEG是正方形.理由如下：
由①知，当∠BAC = 135°时，∠DAG = 90°.
∵四边形ABDI是正方形，
∴AD = $\sqrt{AB^{2}+BD^{2}}=\sqrt{2}AB$.
又四边形ACHG是正方形，
∴AC = AG = $\sqrt{2}AB$，
∴AG = AD.
∴当∠BAC = 135°且AC = $\sqrt{2}AB$时，四边形ADEG是正方形.