2025年单元双测全优测评卷八年级数学下册沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷八年级数学下册沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
21. 将两张完全相同的矩形纸片ABCD,FBED按如图方式放置,BD为重合的对角线,重叠部分为四边形DHBG.
(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB = 8,AD = 4,求四边形DHBG的面积.

(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB = 8,AD = 4,求四边形DHBG的面积.

答案:
(1)菱形.理由如下:
∵四边形ABCD,FBED是完全相同的矩形,
∴∠A=∠E=90°,AD=ED,AB=EB.
∴△DAB≌△DEB(SAS).
∴∠ABD=∠EBD.
∵AB//CD,DF//BE,
∴四边形DHBG是平行四边形,∠HDB =∠EBD.
∴∠HDB=∠HBD.
∴DH=BH.
∴平行四边形DHBG是菱形.
(2)由
(1),设DH=BH=x,则AH=8−x.在Rt△ADH中,AD²+AH²=DH²,即4²+(8−x)²=x²,解得x=5,则BH=5.
∴菱形DHBG的面积为HB·AD=20.
(1)菱形.理由如下:
∵四边形ABCD,FBED是完全相同的矩形,
∴∠A=∠E=90°,AD=ED,AB=EB.
∴△DAB≌△DEB(SAS).
∴∠ABD=∠EBD.
∵AB//CD,DF//BE,
∴四边形DHBG是平行四边形,∠HDB =∠EBD.
∴∠HDB=∠HBD.
∴DH=BH.
∴平行四边形DHBG是菱形.
(2)由
(1),设DH=BH=x,则AH=8−x.在Rt△ADH中,AD²+AH²=DH²,即4²+(8−x)²=x²,解得x=5,则BH=5.
∴菱形DHBG的面积为HB·AD=20.
22. 如图,在矩形ABCD中,AB = 6,BC = 8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.
(1)若点C′刚好落在对角线BD上时,BC′ =________;
(2)当BC′//DE时,求CE的长;
(3)若点C′刚好落在线段AD的垂直平分线上时,求CE的长.
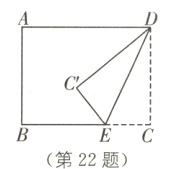
(1)若点C′刚好落在对角线BD上时,BC′ =________;
(2)当BC′//DE时,求CE的长;
(3)若点C′刚好落在线段AD的垂直平分线上时,求CE的长.



答案:
(1)4
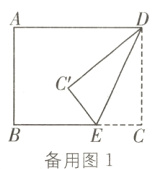
(2)如图
(1),连接BC'.
由折叠,得∠CED=∠C'ED.
∵BC'//DE,
∴∠EC'B=∠C'ED,∠CED=∠C'BE.
∴∠EC'B=∠C'BE.
∴EC=C'E=BE=$\frac{1}{2}$BC=4.
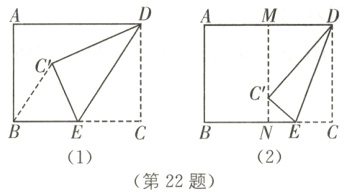
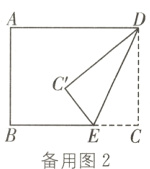
(3)作AD的垂直平分线,交AD于点M,交BC于点N,分两种情况讨论:
①当点C'在矩形内部时,如图
(2),
∵点C'在AD的垂直平分线上,
∴DM=4.
∵DC'=DC=6,
∴由勾股定理,得MC'=$\sqrt{DC'²−DM²}$=2$\sqrt{5}$.
∴NC'=6−2$\sqrt{5}$
设EC=x,则C'E=x,NE=4−x.
∵NC'²+NE²=C'E²,
∴(6−2$\sqrt{5}$)²+(4−x)²=x²,
解得x=9−3$\sqrt{5}$,即CE=9−3$\sqrt{5}$
②当点C'在矩形外部时,如图
(3).
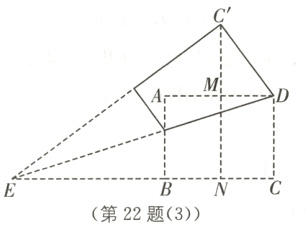
∵点C'在AD的垂直平分线上,
∴DM=4.
∵DC'=6,
∴由勾股定理,得MC'=2$\sqrt{5}$
∴NC'=6+2$\sqrt{5}$
设EC=y,则C'E=y,NE=y−4.
∵NC'²+NE²=C'E²,
∴(6+2$\sqrt{5}$)²+(y−4)²=y²,
解得y=9+3$\sqrt{5}$,即CE=9+3$\sqrt{5}$
综上所述,CE的长为9+3$\sqrt{5}$或9−3$\sqrt{5}$
(1)4
(2)如图
(1),连接BC'.
由折叠,得∠CED=∠C'ED.
∵BC'//DE,
∴∠EC'B=∠C'ED,∠CED=∠C'BE.
∴∠EC'B=∠C'BE.
∴EC=C'E=BE=$\frac{1}{2}$BC=4.

(3)作AD的垂直平分线,交AD于点M,交BC于点N,分两种情况讨论:
①当点C'在矩形内部时,如图
(2),
∵点C'在AD的垂直平分线上,
∴DM=4.
∵DC'=DC=6,
∴由勾股定理,得MC'=$\sqrt{DC'²−DM²}$=2$\sqrt{5}$.
∴NC'=6−2$\sqrt{5}$
设EC=x,则C'E=x,NE=4−x.
∵NC'²+NE²=C'E²,
∴(6−2$\sqrt{5}$)²+(4−x)²=x²,
解得x=9−3$\sqrt{5}$,即CE=9−3$\sqrt{5}$
②当点C'在矩形外部时,如图
(3).

∵点C'在AD的垂直平分线上,
∴DM=4.
∵DC'=6,
∴由勾股定理,得MC'=2$\sqrt{5}$
∴NC'=6+2$\sqrt{5}$
设EC=y,则C'E=y,NE=y−4.
∵NC'²+NE²=C'E²,
∴(6+2$\sqrt{5}$)²+(y−4)²=y²,
解得y=9+3$\sqrt{5}$,即CE=9+3$\sqrt{5}$
综上所述,CE的长为9+3$\sqrt{5}$或9−3$\sqrt{5}$
查看更多完整答案,请扫码查看


