《2025年单元双测全优测评卷八年级数学下册沪科版》

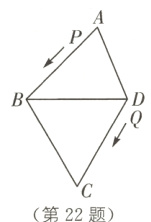
22. 如图，四边形ABCD的三边（AB，BC，CD）和BD的长度都为5厘米，动点P从A出发（A→B→D）到D，速度为2厘米/秒，动点Q从点D出发（D→C→B→A）到A，速度为2.8厘米/秒. 5秒时P，Q相距3厘米，试确定5秒时△APQ的形状.

答案：
$\because AB = BD = 5$厘米,动点$P$从$A$出发$(A\rightarrow B\rightarrow D)$到$D$,速度为2厘米/秒,
$\therefore 5$秒时$P$点运动路程为$2\times5 = 10$(厘米).
又$AB + BD = 10$厘米,
$\therefore$此时$P$与$D$重合.
$\because AB = BC = CD = 5$厘米,动点$Q$从点$D$出发$(D\rightarrow C\rightarrow B\rightarrow A)$到$A$,速度为2.8厘米/秒,$\therefore 5$秒时$Q$点运动路程为$2.8\times5 = 14$(厘米).
又$DC + CB + BA = 15$厘米,
$\therefore Q$在$AB$边上,且$BQ = 4$厘米,如图.

在$\triangle BPQ$中,$\because BQ = 4$厘米,$PQ = 3$厘米,$BP = 5$厘米,$\therefore BQ^{2}+PQ^{2}=BP^{2}$,
$\therefore\triangle BPQ$为直角三角形,$\angle BQP = 90^{\circ}$,
$\therefore\angle AQP = 180^{\circ}-\angle BQP = 90^{\circ}$,
$\therefore\triangle APQ$为直角三角形.

23. 观察下列各式，你有什么发现？
$3^2 = 4 + 5$，$5^2 = 12 + 13$，$7^2 = 24 + 25$，$9^2 = 40 + 41$，…，
这到底是巧合，还是有什么规律蕴涵其中呢？
（1）填空：$13^2 =$_______ + _______；
（2）请写出你发现的规律；
（3）结合勾股定理有关知识，说明你的结论的正确性.

答案：
(1)84 85
(2)任意一个大于1的奇数的平方可以拆成两个连续整数的和$(2n + 1)^{2}=\frac{(2n + 1)^{2}-1}{2}+\frac{(2n + 1)^{2}+1}{2}$,并且这两个连续整数与原来的奇数构成一组勾股数.
(3)$\frac{(2n + 1)^{2}-1}{2}+\frac{(2n + 1)^{2}+1}{2}=\frac{(2n + 1)^{2}+(2n + 1)^{2}-1 + 1}{2}=(2n + 1)^{2}$,
$(2n + 1)^{2}+(\frac{(2n + 1)^{2}-1}{2})^{2}=(2n + 1)^{2}+\frac{(2n + 1)^{4}-2(2n + 1)^{2}+1}{4}=\frac{4(2n + 1)^{2}}{4}+\frac{(2n + 1)^{4}-2(2n + 1)^{2}+1}{4}=(\frac{(2n + 1)^{2}+1}{2})^{2}$.
故结论正确.