《2025年单元双测全优测评卷八年级数学下册沪科版》

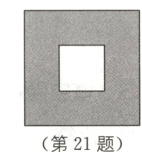
21. 如图，某学校计划在校园内修建一个正方形的花坛，在花坛中央还要修一个正方形的小喷水池. 搞设计需要考虑有关的周长，如果小喷水池的面积为8平方米，花坛的绿化面积为10平方米，问花坛的外周与小喷水池的周长一共是多少米？

答案： 由题意可知喷水池的边长为$\sqrt{8}$米，花坛的外周边长为$\sqrt{10 + 8}=\sqrt{18}$(米)，
所以花坛的外周与小喷水池的周长一共是$4(\sqrt{8}+\sqrt{18})=20\sqrt{2}$(米).

22. 已知$a$，$b$，$m$都是实数，若$a + b = 2$，则称$a$与$b$是关于1的“平衡数”.
（1）$-1$与_______是关于1的“平衡数”，$1-\sqrt{2}$与_______是关于1的“平衡数”；
（2）若$(\sqrt{3}+m)(\sqrt{3}-1)=2$，判断$m+\sqrt{3}$与$2-\sqrt{3}$是否是关于1的“平衡数”，并说明理由.

答案：
(1)3 $1+\sqrt{2}$
(2)$m+\sqrt{3}$与$2-\sqrt{3}$不是关于1的“平衡数”.理由如下：
因为$(\sqrt{3}+m)(\sqrt{3}-1)=2$，
整理，得$(1-\sqrt{3})m = 1-\sqrt{3}$，
解得$m = 1$，则$1+\sqrt{3}+2-\sqrt{3}=3\neq2$，
所以$m+\sqrt{3}$与$2-\sqrt{3}$不是关于1的“平衡数”.

23. 数学教育家波利亚曾说：“对一个数学问题，改变它的形式，变换它的结构，直到发现有价值的东西，这是数学解题的一个重要原则”.
材料一：平方运算和开方运算是互逆运算. 如$a^{2}\pm2ab + b^{2}=(a\pm b)^{2}$，那么$\sqrt{a^{2}\pm2ab + b^{2}}=\vert a\pm b\vert$. 如何将双重二次根式$\sqrt{5\pm2\sqrt{6}}$化简？我们可以把$5\pm2\sqrt{6}$转化为$(\sqrt{3})^{2}\pm2\sqrt{6}+(\sqrt{2})^{2}=(\sqrt{3}\pm\sqrt{2})^{2}$完全平方的形式，因此双重二次根式$\sqrt{5\pm2\sqrt{6}}=\sqrt{(\sqrt{3}\pm\sqrt{2})^{2}}=\sqrt{3}\pm\sqrt{2}$得以化简.
材料二：在平面直角坐标系$xOy$中，对于点$P(x,y)$和$Q(x,y')$给出如下定义：若$y'=\begin{cases}y(x\geqslant0)\\ -y(x＜0)\end{cases}$，则称点$Q$为点$P$的“横负纵变点”. 例如：点$(3,2)$的“横负纵变点”为$(3,2)$，点$(-2,5)$的“横负纵变点”为$(-2,-5)$.
请选择合适的材料解决下面的问题：
（1）点$(\sqrt{2},-\sqrt{3})$的“横负纵变点”为_______，点$(-3\sqrt{3},-2)$的“横负纵变点”为_______；
（2）化简：$\sqrt{7 + 2\sqrt{10}}$；
（3）已知$a$为常数$(1\leqslant a\leqslant2)$，点$M(-\sqrt{2},m)$，且$m=\frac{1}{\sqrt{2}}\times(\sqrt{a + 2\sqrt{a - 1}}+\sqrt{a - 2\sqrt{a - 1}})$，点$M'$是点$M$的“横负纵变点”，则点$M'$的坐标是_______.

答案：
(1)$(\sqrt{2},-\sqrt{3})$ $(-3\sqrt{3},2)$
(2)$\sqrt{7 + 2\sqrt{10}}$
$=\sqrt{(\sqrt{5})^2+2\times\sqrt{5}\times\sqrt{2}+(\sqrt{2})^2}$
$=\sqrt{(\sqrt{5}+\sqrt{2})^2}=\vert\sqrt{5}+\sqrt{2}\vert=\sqrt{5}+\sqrt{2}$.
(3)$(-\sqrt{2},-\sqrt{2})$