《2025年单元双测全优测评卷八年级数学下册沪科版》

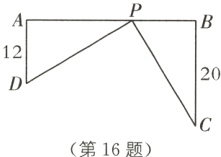
16. 一条东西走向的公路上有A，B两个站点(视为直线上的两点)相距30 km，C，D为两村庄(视为两个点)，DA⊥AB于点A，CB⊥AB于点B(如图)，已知DA = 12 km，CB = 20 km，现在要在公路AB上建一个土特产储藏仓库P，使得C，D两村庄到储藏仓库P的直线距离相等，请求出储藏仓库P到A站点的距离.(精确到1 km)

答案：
∵C，D两村庄到储藏仓库P的直线距离相等，
∴CP = DP.
∵DA⊥AB，CB⊥AB，
∴∠A = ∠B = 90°.
在Rt△APD和Rt△BCP中，由勾股定理，得$DP^{2}=AD^{2}+AP^{2}$，$CP^{2}=BP^{2}+BC^{2}$，
∴$AD^{2}+AP^{2}=BP^{2}+BC^{2}$，
设AP = x km，则BP = (30 - x)km，
∴$12^{2}+x^{2}=(30 - x)^{2}+20^{2}$，解得x≈19.
故储藏仓库P到A站点的距离约为19 km.

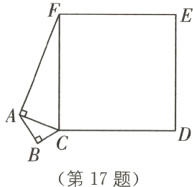
17. 如图，BC长为3，AB长为4，AF长为13，且AB⊥BC，AC⊥AF. 求正方形CDEF的面积.

答案： 在Rt△ABC中，
$AC^{2}=AB^{2}+BC^{2}=3^{2}+4^{2}=25$.
在Rt△FAC中，
$FC^{2}=AF^{2}+AC^{2}=13^{2}+25=194$，
即正方形CDEF的面积为194.

18. 若△ABC的三边长a，b，c满足a² + b² + c² + 338 = 10a + 24b + 26c，试判断△ABC的形状.

答案： 由$a^{2}+b^{2}+c^{2}+338 = 10a + 24b + 26c$，得
$a^{2}-10a + 25 + b^{2}-24b + 144 + c^{2}-26c + 169 = 0$，
即$(a - 5)^{2}+(b - 12)^{2}+(c - 13)^{2}=0$.
∴a = 5，b = 12，c = 13.
∵$5^{2}+12^{2}=13^{2}$，
∴$a^{2}+b^{2}=c^{2}$.
∴∠C = 90°，即△ABC是直角三角形.