《2025年优化探究同步导学案高中物理必修第一册人教版》

1.弹性形变:物体在发生形变后,如果撤去作用力能够恢复原状,这种形变叫作弹性形变。

答案： 1.作用力

2.弹性限度:如果形变过大,超过一定的限度,撤去作用力后物体不能完全恢复原来的形状,这个限度叫作弹性限度。

答案： 2.完全

3.胡克定律
(1)内容:在弹性限度内,弹簧发生弹性形变时,弹力$F$的大小跟弹簧伸长(或缩短)的长度$x$成正比。
(2)表达式:$F=kx$,式中$k$叫作弹簧的劲度系数,单位是牛顿每米,符号是N/m。

答案： 3.
(1)正比　
(2)N/m

4.劲度系数
(1)意义:弹簧的劲度系数大小反映了弹簧的软硬程度。
(2)弹簧劲度系数与弹簧软硬的关系:劲度系数越大,弹簧越硬;劲度系数越小,弹簧越软。

答案： 4.
(1)软硬　
(2)越硬 越软

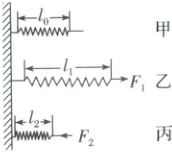
(1)如图所示,图甲表示弹簧处于原长状态,弹簧的原长为$l_0$,图乙在拉力$F_1$的作用下弹簧的长度为$l_1$,图丙在压力$F_2$的作用下弹簧的长度为$l_2$。若图中弹簧的劲度系数为$k$,则$F_1$和$F_2$分别等于多少?

答案： 提示:
(1)在公式F=kx中，x表示的是弹簧伸长的长度或缩短的长度，而不是弹簧的长度。题图乙中弹簧伸长量为$l_1 - l_0，$题图丙中弹簧压缩量为$l_0 - l_2，$所以$F_1 = k(l_1 - l_0)，$$F_2 = k(l_0 - l_2)。$

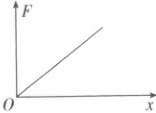
(2)若以弹力和弹簧形变量分别作为纵轴和横轴建立坐标系作$F-x$图像,如图所示,图像的斜率的物理意义是什么?

答案： 提示:
(2)斜率表示弹簧的劲度系数。

(3)不同弹簧的$F-x$图像是否一样?

答案： 提示:
(3)弹簧不一样，劲度系数不同，图线的倾斜程度不同。

[例5] 一根轻质弹簧在$10.0\ N$的拉力作用下,其长度由原来的$5.00\ cm$伸长为$6.00\ cm$。求:(弹簧始终在弹性限度内)
(1)当这根弹簧长度为$4.20\ cm$时,弹簧受到的压力是多大?
(2)当弹簧受到$15.0\ N$的拉力时,弹簧的长度是多少?
[课堂笔记]

答案： [答案]　
(1)8.00 N
(2)6.50 cm
[解析]　
(1)弹簧原长$l_0 = 5.00 cm = 5.00×10^{-2} m $
在拉力$F_1 = 10.0 N$的作用下伸长到$l_1 = 6.00 cm = 6.00×10^{-2} m $
根据胡克定律得$F_1 = kx_1 = k(l_1 - l_0)$
解得弹簧的劲度系数$k = \frac{F_1}{l_1 - l_0} = \frac{10.0}{(6.00 - 5.00)×10^{-2}} N/m = 1.00×10^3 N/m $
设当压力大小为$F_2$时，弹簧被压缩到$l_2 = 4.20 cm = 4.20×10^{-2} m $
根据胡克定律得，压力大小
$F_2 = kx_2 = k(l_0 - l_2) = 1.00×10^3×(5.00 - 4.20)×10^{-2} N = 8.00 N。$
(2)设弹簧的弹力大小F = 15.0 N时弹簧的伸长量为x，由胡克定律得
$x = \frac{F}{k} = \frac{15.0}{1.00×10^3} m = 1.50×10^{-2} m = 1.50 cm $
此时弹簧的长度为$l = l_0 + x = 6.50 cm。$