第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
9. 二次函数$y = ax^{2}+bx + c$($a$,$b$,$c$为常数,$a\neq0$)的自变量$x$与函数$y$对应值如表:
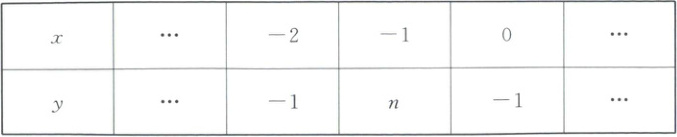
若$n < -1$,则点$A(bc,-a)$所在象限是(
A.第一象限
B.第二象限
C.第三象限
D.第四象限

若$n < -1$,则点$A(bc,-a)$所在象限是(
C
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
9.C 解析:由表格数据可知抛物线开口向上,对称轴为直线x=$\frac{-2 + 0}{2}$=−1,c=−1,
∴a>0,$-\frac{b}{2a}$=−1,c<0,
∴b=2a>0,
∴−a<0,bc<0,
∴点A(bc,−a)在第三象限.
故选:C.
∴a>0,$-\frac{b}{2a}$=−1,c<0,
∴b=2a>0,
∴−a<0,bc<0,
∴点A(bc,−a)在第三象限.
故选:C.
10. 如图,赵爽弦图由四个全等的直角三角形所组成,大正方形$ABCD$中间是一个小正方形$EFGH$.连结$CE$并延长,交$BG$于点$M$,交$AB$于点$N$.连结$NF$,$HM$,若要求出$\triangle ANF$的面积,只需要知道(
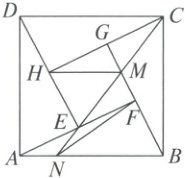
A.$\triangle GHM$的面积
B.$\triangle MNF$的面积
C.$\triangle EMF$的面积
D.$\triangle GCM$的面积
D
)
A.$\triangle GHM$的面积
B.$\triangle MNF$的面积
C.$\triangle EMF$的面积
D.$\triangle GCM$的面积
答案:
10.D 解析:过点N作NP⊥AF于点P,如图所示:

设PN=x,CH=a,CG=b,
依题意,得AF=a,AE=FB=b,GF=FE=a−b,CH//AF,BF⊥AF,
∴CG//EF,
∴△CGM∽△EFM,
∴$\frac{GM}{MF}=\frac{CG}{EF}=\frac{b}{a - b}$,
设GM=bk,MF=(a−b)k,
∵GM+MF=GF=a−b,
∴bk+ak−bk=a−b,
∴k=$\frac{a - b}{a}$,
∴GM=bk=$\frac{b(a - b)}{a}$,MF=(a−b)k=$\frac{(a - b)^2}{a}$,
∴S△GCM=$\frac{1}{2}$CG⋅GM=$\frac{1}{2}$b⋅$\frac{b(a - b)}{a}$=$\frac{b^2(a - b)}{2a}$,
∵NP⊥AF,BF⊥AF,
∴NP//BF,
∴△APN∽△AFB,
∴$\frac{AP}{AF}=\frac{PN}{FB}=\frac{AP}{a}$,
∴AP=$\frac{ax}{b}$,
∴PE=AE−AP=b−$\frac{ax}{b}$=$\frac{b^2 - ax}{b}$,
∵NP//MF,
∴△NPE∽△MFE,
∴$\frac{PN}{MF}=\frac{PE}{FE}$,
∴PN⋅FE=PE⋅MF,
∴x⋅(a−b)=$\frac{b^2 - ax}{b}$⋅$\frac{(a - b)^2}{a}$,
整理,得abx=(a−b)(b²−ax),
∴abx=b²(a−b)−a²x+abx,
∴x=$\frac{b^2(a - b)}{a^2}$,
∴S△ANF=$\frac{1}{2}$AF⋅PN=$\frac{1}{2}$a×$\frac{b^2(a - b)}{a^2}$=$\frac{b^2(a - b)}{2a}$,
∴S△ANF=S△GCM,若要求出△ANF的面积,只需知道△GCM的面积即可.
故选:D.
10.D 解析:过点N作NP⊥AF于点P,如图所示:

设PN=x,CH=a,CG=b,
依题意,得AF=a,AE=FB=b,GF=FE=a−b,CH//AF,BF⊥AF,
∴CG//EF,
∴△CGM∽△EFM,
∴$\frac{GM}{MF}=\frac{CG}{EF}=\frac{b}{a - b}$,
设GM=bk,MF=(a−b)k,
∵GM+MF=GF=a−b,
∴bk+ak−bk=a−b,
∴k=$\frac{a - b}{a}$,
∴GM=bk=$\frac{b(a - b)}{a}$,MF=(a−b)k=$\frac{(a - b)^2}{a}$,
∴S△GCM=$\frac{1}{2}$CG⋅GM=$\frac{1}{2}$b⋅$\frac{b(a - b)}{a}$=$\frac{b^2(a - b)}{2a}$,
∵NP⊥AF,BF⊥AF,
∴NP//BF,
∴△APN∽△AFB,
∴$\frac{AP}{AF}=\frac{PN}{FB}=\frac{AP}{a}$,
∴AP=$\frac{ax}{b}$,
∴PE=AE−AP=b−$\frac{ax}{b}$=$\frac{b^2 - ax}{b}$,
∵NP//MF,
∴△NPE∽△MFE,
∴$\frac{PN}{MF}=\frac{PE}{FE}$,
∴PN⋅FE=PE⋅MF,
∴x⋅(a−b)=$\frac{b^2 - ax}{b}$⋅$\frac{(a - b)^2}{a}$,
整理,得abx=(a−b)(b²−ax),
∴abx=b²(a−b)−a²x+abx,
∴x=$\frac{b^2(a - b)}{a^2}$,
∴S△ANF=$\frac{1}{2}$AF⋅PN=$\frac{1}{2}$a×$\frac{b^2(a - b)}{a^2}$=$\frac{b^2(a - b)}{2a}$,
∴S△ANF=S△GCM,若要求出△ANF的面积,只需知道△GCM的面积即可.
故选:D.
11. 把抛物线$y = 2x^{2}$向上平移1个单位后得到的抛物线表达式是
y=2x²+1
.
答案:
11.y=2x²+1 解析:
∵抛物线y=2x²的顶点坐标是(0,0),
∴平移后的抛物线的顶点坐标是(0,1),
∴得到的抛物线表达式是y=2x²+1.故答案为y=2x²+1.
∵抛物线y=2x²的顶点坐标是(0,0),
∴平移后的抛物线的顶点坐标是(0,1),
∴得到的抛物线表达式是y=2x²+1.故答案为y=2x²+1.
12. 已知线段$a = 8$,$b = 2$,线段$c$是线段$a$,$b$的比例中项,则$c =$
4
.
答案:
12.4 解析:
∵线段c是线段a,b的比例中项,
∴c²=ab,
而线段a=8,b=2,
∴c²=8×2=16,
而c>0,
∴c=4.故答案为4.
∵线段c是线段a,b的比例中项,
∴c²=ab,
而线段a=8,b=2,
∴c²=8×2=16,
而c>0,
∴c=4.故答案为4.
13. “头盔是生命之盔”,质检部门对某工厂生产的头盔质量进行抽查,抽查结果如表:
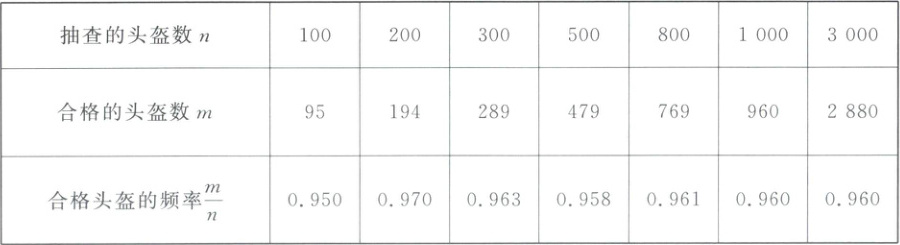
请估计该工厂生产10000个头盔,合格的头盔有

请估计该工厂生产10000个头盔,合格的头盔有
9600
个.
答案:
13.9600 解析:估计该工厂生产10000个头盔,合格的头盔有10000×0.96=9600(个).
故答案为9600.
故答案为9600.
14. 如图,折扇的骨柄长为$30$cm,扇面宽度为$18$cm,折扇张开的角度为$120^{\circ}$,则折扇扇面的面积为
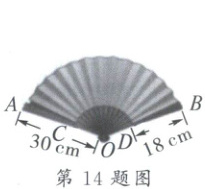
252π
$cm^{2}$.(结果保留$\pi$)
答案:
14.252π 解析:
∵OA=OB=30cm,AC=BD=18cm,
∴OC=OD=30−18=12(cm),
∵折扇张开的角度为120°,
∴折扇扇面的面积为$\frac{120π×30^2}{360}-\frac{120π×12^2}{360}$=252π(cm²).
故答案为252π.
∵OA=OB=30cm,AC=BD=18cm,
∴OC=OD=30−18=12(cm),
∵折扇张开的角度为120°,
∴折扇扇面的面积为$\frac{120π×30^2}{360}-\frac{120π×12^2}{360}$=252π(cm²).
故答案为252π.
15. 设二次函数$y = x^{2}+bx + 2b - 3$,当$-1\leq x\leq2$时,函数有最小值$-15$,则$b$的值为
-4
.
答案:
15.−4 解析:二次函数y=x²+bx+2b−3的对称轴为直线x=$-\frac{b}{2}$,
①当$-\frac{b}{2}$<−1即b>2时,x=−1的函数值最小,y最小=1−b+2b−3=−15,
解得b=−13(舍去);
②当−1⩽$-\frac{b}{2}$⩽2即−4⩽b⩽2时,x=$-\frac{b}{2}$的函数值最小,y最小=$\frac{1}{4}$b²−$\frac{1}{2}$b²+2b−3=−15,
解得b=12(舍去)或b=−4,
③当$-\frac{b}{2}$>2即b<−4时,x=2的函数值最小,y最小=4+2b+2b−3=−15,
解得b=−4(舍去),综上,b的值为−4.
故答案为−4.
①当$-\frac{b}{2}$<−1即b>2时,x=−1的函数值最小,y最小=1−b+2b−3=−15,
解得b=−13(舍去);
②当−1⩽$-\frac{b}{2}$⩽2即−4⩽b⩽2时,x=$-\frac{b}{2}$的函数值最小,y最小=$\frac{1}{4}$b²−$\frac{1}{2}$b²+2b−3=−15,
解得b=12(舍去)或b=−4,
③当$-\frac{b}{2}$>2即b<−4时,x=2的函数值最小,y最小=4+2b+2b−3=−15,
解得b=−4(舍去),综上,b的值为−4.
故答案为−4.
16. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 3$,$BC = 4$.斜边$AB$上一点$E$满足$AC = AE$,连结$EC$.
(1)$CE$的长为
(2)$F$是射线$CE$上的点,连结$BF$,$\triangle BEF$的一个内角与$\angle A$相等,则$EF$的长为
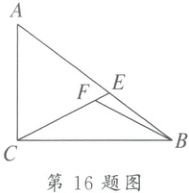
(1)$CE$的长为
$\frac{6\sqrt{5}}{5}$
;(2)$F$是射线$CE$上的点,连结$BF$,$\triangle BEF$的一个内角与$\angle A$相等,则$EF$的长为
$\frac{\sqrt{5}}{5}$或$\frac{4\sqrt{5}}{5}$
.
答案:
16.
(1)$\frac{6\sqrt{5}}{5}$
(2)$\frac{\sqrt{5}}{5}$或$\frac{4\sqrt{5}}{5}$ 解析:
(1)过点C作CD⊥AB于点D,如图1所示:

在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
由勾股定理,得AB=$\sqrt{AC^2+BC^2}$=5,
由三角形的面积公式,得S△ABC=$\frac{1}{2}$AB⋅CD=$\frac{1}{2}$AC⋅BC,
∴CD=$\frac{AC⋅BC}{AB}$=$\frac{3×4}{5}$=$\frac{12}{5}$,
在Rt△ACD中,由勾股定理,得AD=$\sqrt{AC^2−CD^2}$=$\sqrt{3^2−(\frac{12}{5})^2}$=$\frac{9}{5}$,
∵AC=AE=3,
∴DE=AE−AD=3−$\frac{9}{5}$=$\frac{6}{5}$,
在Rt△CDE中,由勾股定理,得CE=$\sqrt{CD^2+DE^2}$=$\sqrt{(\frac{12}{5})^2+(\frac{6}{5})^2}$=$\frac{6\sqrt{5}}{5}$.故答案为$\frac{6\sqrt{5}}{5}$.
(2)
∵∠CEB是△ACE的一个外角,
∴∠CEB>∠A,当点F在射线CE上,△BEF的一个内角与∠A相等时,有以下两种情况:
①当∠EFB=∠A时,过点A作AK⊥CE于点K,过点B作BH⊥CE,交CE的延长线于点H,如图2所示:

∴AK//BH,
由
(1)可知,BC=4,AB=5,AC=AE=3,CD=$\frac{12}{5}$,CE=$\frac{6\sqrt{5}}{5}$,
∴BE=AB−AE=2,
由三角形的面积公式,得S△ACE=$\frac{1}{2}$CE⋅AK=$\frac{1}{2}$AE⋅CD,
∴$\frac{1}{2}$×$\frac{6\sqrt{5}}{5}$×AK=$\frac{1}{2}$×3×$\frac{12}{5}$,
∴AK=$\frac{6\sqrt{5}}{5}$,
∵AK//BH,
∴△AKE∽△BHE,
∴$\frac{AK}{BH}=\frac{AE}{BE}$,
∴AE⋅BH=AK⋅BE,
∴3×BH=$\frac{6\sqrt{5}}{5}$×2,
∴BH=$\frac{4\sqrt{5}}{5}$,
在Rt△BHE中,由勾股定理,
得EH=$\sqrt{BE^2−BH^2}$=$\sqrt{2^2−(\frac{4\sqrt{5}}{5})^2}$=$\frac{2\sqrt{5}}{5}$,
在△FBH和△ABC中,∠EFB=∠A,∠H=∠ACB=90°,
∴△FBH∽△ABC,
∴$\frac{FH}{AC}=\frac{BH}{BC}$,
∴FH⋅BC=BH⋅AC,
∴FH×4=$\frac{4\sqrt{5}}{5}$×3,
∴FH=$\frac{3\sqrt{5}}{5}$,
∴EF=FH−EH=$\frac{3\sqrt{5}}{5}$−$\frac{2\sqrt{5}}{5}$=$\frac{\sqrt{5}}{5}$;
②当∠EBF=∠A时,过点B作BH⊥EF于点H,如图3所示:

∴AC//BF,
∴∠ACE=∠F,
∵AC=AE,
∴∠ACE=∠AEC,
∴∠AEC=∠F,
又
∵∠AEC=∠BEF,
∴∠BEF=∠F,
∴BF=BE=2,
∵BH⊥EF,
∴EH=FH,即EF=2EH,由①可知EH=$\frac{2\sqrt{5}}{5}$,
∴EF=2EH=$\frac{4\sqrt{5}}{5}$,
综上所述,EF的长为$\frac{\sqrt{5}}{5}$或$\frac{4\sqrt{5}}{5}$.
故答案为$\frac{\sqrt{5}}{5}$或$\frac{4\sqrt{5}}{5}$.
16.
(1)$\frac{6\sqrt{5}}{5}$
(2)$\frac{\sqrt{5}}{5}$或$\frac{4\sqrt{5}}{5}$ 解析:
(1)过点C作CD⊥AB于点D,如图1所示:

在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
由勾股定理,得AB=$\sqrt{AC^2+BC^2}$=5,
由三角形的面积公式,得S△ABC=$\frac{1}{2}$AB⋅CD=$\frac{1}{2}$AC⋅BC,
∴CD=$\frac{AC⋅BC}{AB}$=$\frac{3×4}{5}$=$\frac{12}{5}$,
在Rt△ACD中,由勾股定理,得AD=$\sqrt{AC^2−CD^2}$=$\sqrt{3^2−(\frac{12}{5})^2}$=$\frac{9}{5}$,
∵AC=AE=3,
∴DE=AE−AD=3−$\frac{9}{5}$=$\frac{6}{5}$,
在Rt△CDE中,由勾股定理,得CE=$\sqrt{CD^2+DE^2}$=$\sqrt{(\frac{12}{5})^2+(\frac{6}{5})^2}$=$\frac{6\sqrt{5}}{5}$.故答案为$\frac{6\sqrt{5}}{5}$.
(2)
∵∠CEB是△ACE的一个外角,
∴∠CEB>∠A,当点F在射线CE上,△BEF的一个内角与∠A相等时,有以下两种情况:
①当∠EFB=∠A时,过点A作AK⊥CE于点K,过点B作BH⊥CE,交CE的延长线于点H,如图2所示:

∴AK//BH,
由
(1)可知,BC=4,AB=5,AC=AE=3,CD=$\frac{12}{5}$,CE=$\frac{6\sqrt{5}}{5}$,
∴BE=AB−AE=2,
由三角形的面积公式,得S△ACE=$\frac{1}{2}$CE⋅AK=$\frac{1}{2}$AE⋅CD,
∴$\frac{1}{2}$×$\frac{6\sqrt{5}}{5}$×AK=$\frac{1}{2}$×3×$\frac{12}{5}$,
∴AK=$\frac{6\sqrt{5}}{5}$,
∵AK//BH,
∴△AKE∽△BHE,
∴$\frac{AK}{BH}=\frac{AE}{BE}$,
∴AE⋅BH=AK⋅BE,
∴3×BH=$\frac{6\sqrt{5}}{5}$×2,
∴BH=$\frac{4\sqrt{5}}{5}$,
在Rt△BHE中,由勾股定理,
得EH=$\sqrt{BE^2−BH^2}$=$\sqrt{2^2−(\frac{4\sqrt{5}}{5})^2}$=$\frac{2\sqrt{5}}{5}$,
在△FBH和△ABC中,∠EFB=∠A,∠H=∠ACB=90°,
∴△FBH∽△ABC,
∴$\frac{FH}{AC}=\frac{BH}{BC}$,
∴FH⋅BC=BH⋅AC,
∴FH×4=$\frac{4\sqrt{5}}{5}$×3,
∴FH=$\frac{3\sqrt{5}}{5}$,
∴EF=FH−EH=$\frac{3\sqrt{5}}{5}$−$\frac{2\sqrt{5}}{5}$=$\frac{\sqrt{5}}{5}$;
②当∠EBF=∠A时,过点B作BH⊥EF于点H,如图3所示:

∴AC//BF,
∴∠ACE=∠F,
∵AC=AE,
∴∠ACE=∠AEC,
∴∠AEC=∠F,
又
∵∠AEC=∠BEF,
∴∠BEF=∠F,
∴BF=BE=2,
∵BH⊥EF,
∴EH=FH,即EF=2EH,由①可知EH=$\frac{2\sqrt{5}}{5}$,
∴EF=2EH=$\frac{4\sqrt{5}}{5}$,
综上所述,EF的长为$\frac{\sqrt{5}}{5}$或$\frac{4\sqrt{5}}{5}$.
故答案为$\frac{\sqrt{5}}{5}$或$\frac{4\sqrt{5}}{5}$.
查看更多完整答案,请扫码查看


