《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

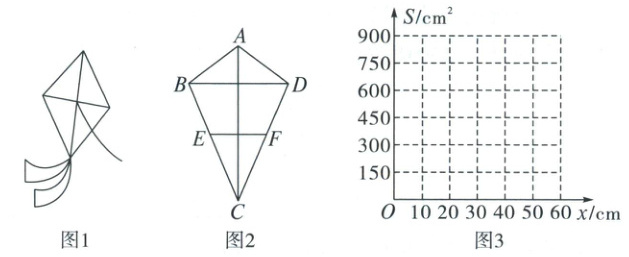
22. （10分）如图1所示风筝的筝面可以抽象成图2的筝形$ABCD$，$AB = AD$，$CB = CD$，风筝的骨架由3条竹棒$AC$，$BD$，$EF$组成，其中$E$，$F$分别是$CB$和$CD$的中点。现有一根总长为90cm的竹棒可截成三段做风筝的骨架。为合理利用筝面$ABCD$的材料，作了如下探究：
（1）设筝面$ABCD$的面积为$S(cm^{2})$，骨架$BD$的长度为$x(cm)$，求$S$关于$x$的函数关系式；
（2）在图3中画出（1）中$S$关于$x$的函数图象；
（3）利用图象分析，当骨架$AC$长度大于$BD$长度且筝面的面积超过$432 cm^{2}$时，求骨架$BD$的长度范围。

答案：
22.解：
(1)
∵$AB = AD$，$CB = CD$，
∴$AC$是$BD$的垂直平分线.
∵$E$，$F$分别是$CB$和$CD$的中点，
∴$EF = \frac{1}{2}BD$，
∵筝面$ABCD$的面积为$S(cm^{2})$，骨架$BD$的长度为$x(cm)$，
∴$S = \frac{1}{2} · AC · BD = \frac{1}{2}(90 - \frac{3}{2}x)x = -\frac{3}{4}x^{2}+45x(0 ＜ x ＜ 60)$.
(2)$S = -\frac{3}{4}x^{2}+45x = -\frac{3}{4}(x - 30)^{2}+675(0 ＜ x ＜ 60)$，
∴当$x = 30$时，$S$取得最大值$675$；
当$y = 0$时，得$-\frac{3}{4}(x - 30)^{2}+675 = 0$，解得$x_{1} = 0$，$x_{2} = 60$，
∴$S$关于$x$的函数的图象如图所示.

(3)当$S = 432$时，$-\frac{3}{4}x^{2}+45x = 432$，解得$x = 12$或$48$，
由$AC ＞ BD$，得$90 - \frac{3}{2}x ＞ x$，解得$x ＜ 36$，
∴当$12 ＜ BD ＜ 36$时，筝面的面积超过$432\ cm^{2}$.

23. （10分）如下表格是抛物线$y = ax^{2}+bx+c$上部分点$(x,y)$的横、纵坐标信息。

（1）若$m = n$，该函数有最大值还是最小值？请作出判断并写出最值；
（2）若$a = -4$，请通过计算判断$p$与$q$的大小关系；
（3）若点$(x,y)$在抛物线上，当$-1\leq x\leq2$时，$-8\leq y\leq7$，求$a$的取值范围。

答案： 23.解：
(1)若$m = n$，该函数有最小值；最小值为$-8$.理由如下：
∵$m = n$，
∴当$x = -2$和当$x = 0$时的函数值相等，
∴对称轴为直线$x = \frac{-2 + 0}{2} = -1$，
∵$-8 ＜ 7$，$x = -1$时的函数值小于$x = 2$时的函数值，
∴该函数有最小值，最小值为$-8$.
(2)由表中数据可知，抛物线$y = ax^{2}+bx + c$经过$(-1,-8)$，$(2,7)$，将$(-1,-8)$，$(2,7)$分别代入，得$\begin{cases} a - b + c = -8 \\ 4a + 2b + c = 7 \end{cases}$，解得$\begin{cases} b = -a + 5 \\ c = -2a - 3 \end{cases}$，把$a = -4$代入，
得$\begin{cases} b = 9 \\ c = 5 \end{cases}$
∴此时抛物线的函数解析式为$y = -4x^{2}+9x + 5$，
当$x = 1$时，$y = -4x^{2}+9x + 5 = -4 + 9 + 5 = 10$；
当$x = 3$时，$y = -4x^{2}+9x + 5 = -4 × 9 + 9 × 3 + 5 = -4$，
∴$p = 10$，$q = -4$，
∴$p ＞ q$.
(3)由题意，得抛物线对称轴为直线$x = -\frac{b}{2a} = \frac{-a + 5}{2a}$.
①当$-\frac{b}{2a} \leq -1$时，若$a ＞ 0$，则当$x \geq -1$时，$y$随$x$增大而增大，
∵当$-1 \leq x \leq 2$时，$-8 \leq y \leq 7$，
∴此时满足题意，
∴$\frac{a - 5}{2a} \leq -1$，
∴$a \leq \frac{5}{3}$，
∴$0 ＜ a \leq \frac{5}{3}$；
若$a ＜ 0$，则当$x \geq -1$时，$y$随$x$的增大而减小，
∵当$-1 \leq x \leq 2$时，$-8 \leq y \leq 7$，
∴此时不满足题意；
②当$-\frac{b}{2a} \geq 2$时若$a ＜ 0$，则当$x \leq 2$时，$y$随$x$的增大而增大，
∵当$-1 \leq x \leq 2$时，$-8 \leq y \leq 7$，
∴此时满足题意，
∴$\frac{a - 5}{2a} \geq 2$，
∴$-\frac{5}{3} \leq a$，
∴$-\frac{5}{3} \leq a ＜ 0$；
若$a ＞ 0$，则当$x \leq 2$时，$y$随$x$增大而减小，
∵当$-1 \leq x \leq 2$时，$-8 \leq y \leq 7$，
∴此时不满足题意；
当$-1 ＜ -\frac{b}{2a} ＜ 2$时，若$a ＞ 0$，则当$-1 \leq x \leq 2$时，函数的最小值一定小于$-8$，若$a ＜ 0$，则当$-1 \leq x \leq 2$时，函数的最大值一定大于$7$，故此种情况不符合题意；
综上所述，$a$的取值范围为$-\frac{5}{3} \leq a ＜ 0$或$0 ＜ a \leq \frac{5}{3}$.