《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

14. 在一个不透明的盒子里装有黑、白两种颜色的球，这些球除颜色外都相同. 小颖做摸球试验，搅匀后，她从盒子里随机摸出一只球记下颜色后，再把球放回盒子中，不断重复上述过程，如表是试验中的部分统计数据：

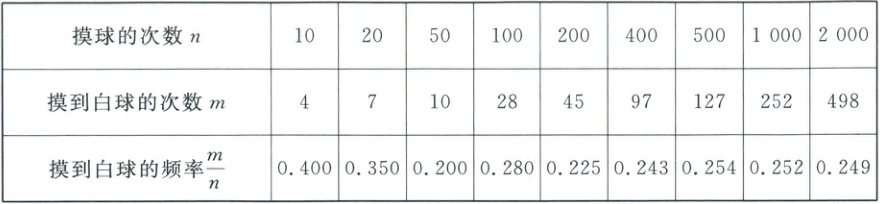
(1) 摸到白球的概率的估计值是0.25(精确到 0.01)；
(2) 若盒子中一共有 60 个球，要使摸到白球的概率为 $\frac{2}{5}$，需要往盒子里再放入多少个白球；
(3) 某小组进行“用频率估计概率”的试验，符合(1)中结果的试验最有可能的是②(填序号).
①投掷一枚均匀的硬币，落到桌面上恰好是正面朝上.
②甲、乙、丙、丁四人用抽签的方式产生一名幸运观众，正好抽到甲.
③掷一个质地均匀的正方体骰子(面的点数分别为 1 到 6，落地时面朝上点数“小于 3”.

答案： 14.解:
(1)根据题意，得大量重复试验下，摸到白球的频率稳定在0.25附近，摸到白球的概率的估计值是0.25.故答案为0.25.
(2)设需要往盒子里再放入x个白球，
根据题意，得(60 + x)×$\frac{2}{5}$ = 60×0.25 + x，
解得x = 15，
即需要往盒子里再放入15个白球.
(3)①投掷一枚均匀的硬币，落到桌面上恰好是正面朝上的概率是$\frac{1}{2}$;
②甲、乙、丙、丁四人用抽签的方式产生一名幸运观众，正好抽到甲的概率是$\frac{1}{4}$ = 0.25;
③掷一个质地均匀的正方体骰子(面的点数分别为1到6)，落地时面朝上点数“小于3”的概率是$\frac{2}{6}$=$\frac{1}{3}$.
则符合
(1)中结果的试验最有可能的是②.
故答案为②.