第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 下列函数对应的抛物线中,形状与抛物线$y = 2x^{2}+3$相同的是(
A.$y = -2x^{2}+3$
B.$y = 3x^{2}+2$
C.$y = -3x^{2}-2$
D.$y = 4x^{2}-2$
A
)A.$y = -2x^{2}+3$
B.$y = 3x^{2}+2$
C.$y = -3x^{2}-2$
D.$y = 4x^{2}-2$
答案:
1.A 解析:
∵抛物线图象的形状只与$|a|$的大小有关,
∴$y = -2x^{2}+3$与抛物线$y = 2x^{2}+3$的形状相同.故选:A.
∵抛物线图象的形状只与$|a|$的大小有关,
∴$y = -2x^{2}+3$与抛物线$y = 2x^{2}+3$的形状相同.故选:A.
2. 下列事件中,属于随机事件的是(
A.普通无人机飞行1小时到月球
B.一个人奔跑速度是每秒500米
C.将普通的冷水加热后水温上升
D.篮球队员投一次篮球正好投中
D
)A.普通无人机飞行1小时到月球
B.一个人奔跑速度是每秒500米
C.将普通的冷水加热后水温上升
D.篮球队员投一次篮球正好投中
答案:
2.D 解析:A.是不可能事件,不符合题意;B.是不可能事件,不符合题意;C.是必然事件,不符合题意;D.是随机事件,符合题意.故选:D.
3. 以矩形$ABCD$的对角线$AC$为直径作圆,则下列说法正确的是(
A.点$B$在圆内
B.点$B$在圆外
C.点$D$在圆上
D.点$D$在圆内
C
)A.点$B$在圆内
B.点$B$在圆外
C.点$D$在圆上
D.点$D$在圆内
答案:
3.C 解析:连结$BD$,如图所示,

由四边形$ABCD$是矩形可知$AC = BD$,$BD$也是以矩形$ABCD$的对角线$AC$为直径的圆的直径,
∴点$B$,$D$都在圆上.
故选:C.
3.C 解析:连结$BD$,如图所示,

由四边形$ABCD$是矩形可知$AC = BD$,$BD$也是以矩形$ABCD$的对角线$AC$为直径的圆的直径,
∴点$B$,$D$都在圆上.
故选:C.
4. 将抛物线$y = x^{2}$先向左平移2个单位,再向下平移3个单位后所得抛物线的解析式为(
A.$y = (x - 2)^{2}+3$
B.$y = (x - 2)^{2}-3$
C.$y = (x + 2)^{2}+3$
D.$y = (x + 2)^{2}-3$
D
)A.$y = (x - 2)^{2}+3$
B.$y = (x - 2)^{2}-3$
C.$y = (x + 2)^{2}+3$
D.$y = (x + 2)^{2}-3$
答案:
4.D 解析:抛物线$y = x^{2}$的顶点坐标为$(0,0)$,把点$(0,0)$先向左平移$2$个单位,再向下平移$3$个单位得到对应点的坐标为$(-2,-3)$,所以平移后的抛物线的解析式为$y=(x + 2)^{2}-3$.
故选:D.
故选:D.
5. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\sin B = \frac{3}{5}$,$AB = 10$,则$BC$的长是(
A.6
B.8
C.$6\sqrt{3}$
D.$8\sqrt{3}$
B
)A.6
B.8
C.$6\sqrt{3}$
D.$8\sqrt{3}$
答案:
5.B 解析:在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\sin B=\frac{3}{5}$,$AB = 10$,
∴$\frac{AC}{10}=\frac{3}{5}$,解得$AC = 6$.
由勾股定理,得$BC = \sqrt{AB^{2}-AC^{2}} = \sqrt{10^{2}-6^{2}} = 8$.
故选:B.
∴$\frac{AC}{10}=\frac{3}{5}$,解得$AC = 6$.
由勾股定理,得$BC = \sqrt{AB^{2}-AC^{2}} = \sqrt{10^{2}-6^{2}} = 8$.
故选:B.
6. 如图,$\triangle ABC$与$\triangle A_{1}B_{1}C_{1}$是位似图形,位似中心为点$O$。若$\triangle ABC$的面积为$40 cm^{2}$,$OB:BB_{1}=2:3$,则$\triangle A_{1}B_{1}C_{1}$的面积是(
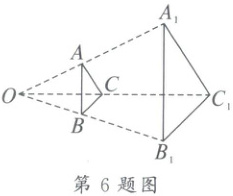
A.$60 cm^{2}$
B.$90 cm^{2}$
C.$100 cm^{2}$
D.$250 cm^{2}$
D
)
A.$60 cm^{2}$
B.$90 cm^{2}$
C.$100 cm^{2}$
D.$250 cm^{2}$
答案:
6.D 解析:
∵$\triangle ABC$与$\triangle A_{1}B_{1}C_{1}$是位似图形,位似中心为点$O$,
∴$\triangle ABC \backsim \triangle A_{1}B_{1}C_{1}$,$AB // A_{1}B_{1}$,
∴$\triangle OAB \backsim$
$\triangle OA_{1}B_{1}$,
∴$\frac{AB}{A_{1}B_{1}}=\frac{OB}{OB_{1}}$.
∵$\triangle ABC$的面积为$40\ cm^{2}$,$OB:BB_{1}=2:3$,
∴$\frac{OB}{OB_{1}}=\frac{2}{5}$,
∴$\frac{AB}{A_{1}B_{1}}=\frac{2}{5}$,
∴$\frac{S_{\triangle ABC}}{S_{\triangle A_{1}B_{1}C_{1}}}=(\frac{AB}{A_{1}B_{1}})^{2}=\frac{4}{25}$,
∴$\frac{40}{S_{\triangle A_{1}B_{1}C_{1}}}=\frac{4}{25}$,
∴$\triangle A_{1}B_{1}C_{1}$的面积是$250\ cm^{2}$.故选:D.
∵$\triangle ABC$与$\triangle A_{1}B_{1}C_{1}$是位似图形,位似中心为点$O$,
∴$\triangle ABC \backsim \triangle A_{1}B_{1}C_{1}$,$AB // A_{1}B_{1}$,
∴$\triangle OAB \backsim$
$\triangle OA_{1}B_{1}$,
∴$\frac{AB}{A_{1}B_{1}}=\frac{OB}{OB_{1}}$.
∵$\triangle ABC$的面积为$40\ cm^{2}$,$OB:BB_{1}=2:3$,
∴$\frac{OB}{OB_{1}}=\frac{2}{5}$,
∴$\frac{AB}{A_{1}B_{1}}=\frac{2}{5}$,
∴$\frac{S_{\triangle ABC}}{S_{\triangle A_{1}B_{1}C_{1}}}=(\frac{AB}{A_{1}B_{1}})^{2}=\frac{4}{25}$,
∴$\frac{40}{S_{\triangle A_{1}B_{1}C_{1}}}=\frac{4}{25}$,
∴$\triangle A_{1}B_{1}C_{1}$的面积是$250\ cm^{2}$.故选:D.
7. 在平面直角坐标系中,将点$A(-4,2)$绕原点$O$顺时针旋转$90^{\circ}$,则点$A$的对应点$A'$的坐标是(
A.$(2,4)$
B.$(4,2)$
C.$(-4,-2)$
D.$(-4,2)$
A
)A.$(2,4)$
B.$(4,2)$
C.$(-4,-2)$
D.$(-4,2)$
答案:
7.A 解析:在平面直角坐标系中,将点$A(-4,2)$绕原点$O$顺时针旋转$90^{\circ}$,如图,过点$A$作$AB \perp x$轴于点$B$,过点$A'$作$A'C \perp x$轴于点$C$,

∴$\angle AOA' = 90^{\circ}$,$OA = OA'$,
∴$\angle AOB + \angle A'OC = 90^{\circ}$.
∵$AB \perp x$轴,$A'C \perp x$轴,
∴$\angle ABO = \angle A'CO = 90^{\circ}$,
∴$\angle A + \angle AOB = 90^{\circ}$,
∴$\angle A = \angle A'OC$.
在$\triangle AOB$和$\triangle OA'C$中,$\begin{cases} \angle A = \angle A'OC \\ \angle ABO = \angle OCA' \\ OA = A'O \end{cases}$
∴$\triangle AOB \cong \triangle OA'C(AAS)$,
∴$AB = OC$,$OB = A'C$.
∵$A(-4,2)$,
∴$OB = 4$,$AB = 2$,
∴$OC = 2$,$A'C = 4$,
∴$A'(2,4)$.
故选:A.
7.A 解析:在平面直角坐标系中,将点$A(-4,2)$绕原点$O$顺时针旋转$90^{\circ}$,如图,过点$A$作$AB \perp x$轴于点$B$,过点$A'$作$A'C \perp x$轴于点$C$,

∴$\angle AOA' = 90^{\circ}$,$OA = OA'$,
∴$\angle AOB + \angle A'OC = 90^{\circ}$.
∵$AB \perp x$轴,$A'C \perp x$轴,
∴$\angle ABO = \angle A'CO = 90^{\circ}$,
∴$\angle A + \angle AOB = 90^{\circ}$,
∴$\angle A = \angle A'OC$.
在$\triangle AOB$和$\triangle OA'C$中,$\begin{cases} \angle A = \angle A'OC \\ \angle ABO = \angle OCA' \\ OA = A'O \end{cases}$
∴$\triangle AOB \cong \triangle OA'C(AAS)$,
∴$AB = OC$,$OB = A'C$.
∵$A(-4,2)$,
∴$OB = 4$,$AB = 2$,
∴$OC = 2$,$A'C = 4$,
∴$A'(2,4)$.
故选:A.
8. 在圆内接四边形$ABCD$中,$AB = AD$,$BD$是对角线,$\angle ABD = 40^{\circ}$,则$\angle C$的度数是(
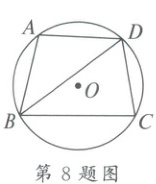
A.$50^{\circ}$
B.$60^{\circ}$
C.$80^{\circ}$
D.$100^{\circ}$
C
)
A.$50^{\circ}$
B.$60^{\circ}$
C.$80^{\circ}$
D.$100^{\circ}$
答案:
8.C 解析:由条件可知$\angle ADB = \angle ABD = 40^{\circ}$,
∴$\angle BAD = 180^{\circ}-\angle ABD - \angle ADB = 100^{\circ}$,
∴$\angle C = 180^{\circ}-\angle BAD = 80^{\circ}$.
故选:C.
∴$\angle BAD = 180^{\circ}-\angle ABD - \angle ADB = 100^{\circ}$,
∴$\angle C = 180^{\circ}-\angle BAD = 80^{\circ}$.
故选:C.
9. 如图,在$5×4$的正方形网格中,点$A$,$B$,$C$,$D$都是网格的格点,$G$是$\triangle ABC$的重心,则下列说法正确的是(
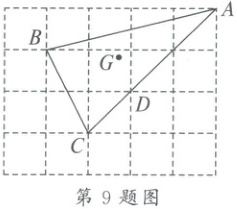
A.连结$DG$,则$DG=\frac{1}{4}BC$
B.连结$BG$,$CG$,则$\angle BGC = 2\angle A$
C.连结$DG$,则$DG// BC$
D.连结$AG$,$BG$,则$S_{\triangle ABG}=\frac{1}{4}S_{\triangle ABC}$
C
)
A.连结$DG$,则$DG=\frac{1}{4}BC$
B.连结$BG$,$CG$,则$\angle BGC = 2\angle A$
C.连结$DG$,则$DG// BC$
D.连结$AG$,$BG$,则$S_{\triangle ABG}=\frac{1}{4}S_{\triangle ABC}$
答案:
9.C 解析:在$5 × 4$的正方形网格中,点$A$,$B$,$C$,$D$都是网格的格点,点$G$是$\triangle ABC$的重心,如图,连结$AG$并延长,交$BC$于点$N$,连结$DG$,

∴$\frac{AG}{AN}=\frac{2}{3}$,$BN = CN$,由图形可得$\frac{AD}{AC}=\frac{2}{3}$,则$\frac{AG}{AN}$
$=\frac{AD}{AC}$.
∵$\angle GAD = \angle NAC$,
∴$\triangle AGD \backsim \triangle ANC$,
∴$\angle AGD = \angle ANC$,$\frac{DG}{CN}=\frac{AD}{AC}=\frac{2}{3}$,
∴$DG // BC$,$DG =$
$\frac{2}{3}CN$,
故C说法正确,符合题意;
∴$DG = \frac{2}{3}CN = \frac{1}{3}BC$,故A说法错误,不符合题意;
∵$\frac{AG}{AN}=\frac{2}{3}$,$BN = CN$,
∴$S_{\triangle ABG}=\frac{2}{3}S_{\triangle ABN}=\frac{2}{3}S_{\triangle ACN}$,
∴$S_{\triangle ABG}=\frac{1}{3}S_{\triangle ABC}$,故D说法错误,不符合题意;
∵$\angle BGN = \angle GBA + \angle GAB$,$\angle CGN = \angle CAG +$
$\angle GCA$,
∴$\angle BGC = \angle GBA + \angle GCA + \angle BAC \neq$
$2\angle BAC$,
故B说法错误,不符合题意.故选:C.
9.C 解析:在$5 × 4$的正方形网格中,点$A$,$B$,$C$,$D$都是网格的格点,点$G$是$\triangle ABC$的重心,如图,连结$AG$并延长,交$BC$于点$N$,连结$DG$,

∴$\frac{AG}{AN}=\frac{2}{3}$,$BN = CN$,由图形可得$\frac{AD}{AC}=\frac{2}{3}$,则$\frac{AG}{AN}$
$=\frac{AD}{AC}$.
∵$\angle GAD = \angle NAC$,
∴$\triangle AGD \backsim \triangle ANC$,
∴$\angle AGD = \angle ANC$,$\frac{DG}{CN}=\frac{AD}{AC}=\frac{2}{3}$,
∴$DG // BC$,$DG =$
$\frac{2}{3}CN$,
故C说法正确,符合题意;
∴$DG = \frac{2}{3}CN = \frac{1}{3}BC$,故A说法错误,不符合题意;
∵$\frac{AG}{AN}=\frac{2}{3}$,$BN = CN$,
∴$S_{\triangle ABG}=\frac{2}{3}S_{\triangle ABN}=\frac{2}{3}S_{\triangle ACN}$,
∴$S_{\triangle ABG}=\frac{1}{3}S_{\triangle ABC}$,故D说法错误,不符合题意;
∵$\angle BGN = \angle GBA + \angle GAB$,$\angle CGN = \angle CAG +$
$\angle GCA$,
∴$\angle BGC = \angle GBA + \angle GCA + \angle BAC \neq$
$2\angle BAC$,
故B说法错误,不符合题意.故选:C.
查看更多完整答案,请扫码查看


