第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
20. (8分)如图,已知 $ \odot O $ 的半径为2,弦 $ CD \perp $ 直径 $ AB $,垂足为 $ E $,点 $ F $ 在 $ \overset{\frown}{AC} $ 上(不与点 $ A $,$ C $ 重合),连结 $ AF $,$ AC $,$ AD $,$ FC $。
(1)求证:$ AC = AD $;
(2)若 $ \angle AFC = \frac{5}{3} \angle ACD $。
① 求 $ \angle ACD $ 的度数;
② 当 $ FC // AD $ 时,求 $ \overset{\frown}{AF} $ 的长。
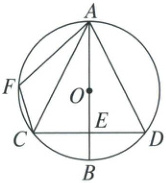
(1)求证:$ AC = AD $;
(2)若 $ \angle AFC = \frac{5}{3} \angle ACD $。
① 求 $ \angle ACD $ 的度数;
② 当 $ FC // AD $ 时,求 $ \overset{\frown}{AF} $ 的长。

答案:
20.
(1)证明:$\because$弦$CD\perp$直径$AB$,$\therefore$点$A$平分$\overset\frown{CAD}$,即$\overset\frown{AC}=\overset\frown{AD}$,$\therefore AC=AD$.
(2)解:①$\because$四边形$AFCD$内接于$\odot O$,$\therefore\angle AFC+\angle ADC=180^{\circ}$,
$\because AC=AD$,$\therefore\angle ACD=\angle ADC$,$\therefore\angle AFC=\frac{5}{3}\angle ACD=\frac{5}{3}\angle ADC$,由上可得$\angle ADC=67.5^{\circ}$,$\therefore\angle ACD=67.5^{\circ}$.
②连结$OC$,$OD$,如图,

$\because\angle ADC=\angle ACD=67.5^{\circ}$,$\therefore\angle CAD=180^{\circ}-2×67.5^{\circ}=45^{\circ}$,$\therefore\angle COD=90^{\circ}$,
$\because FC// AD$,$\therefore\angle AFC+\angle DAF=180^{\circ}$,$\therefore\angle DAF=\angle ADC$,$\overset\frown{AF}=\overset\frown{CD}$.
$\because CD$的长为$\frac{90\pi×2}{180}=\pi$,$\therefore\overset\frown{AF}$的长为$\pi$.
20.
(1)证明:$\because$弦$CD\perp$直径$AB$,$\therefore$点$A$平分$\overset\frown{CAD}$,即$\overset\frown{AC}=\overset\frown{AD}$,$\therefore AC=AD$.
(2)解:①$\because$四边形$AFCD$内接于$\odot O$,$\therefore\angle AFC+\angle ADC=180^{\circ}$,
$\because AC=AD$,$\therefore\angle ACD=\angle ADC$,$\therefore\angle AFC=\frac{5}{3}\angle ACD=\frac{5}{3}\angle ADC$,由上可得$\angle ADC=67.5^{\circ}$,$\therefore\angle ACD=67.5^{\circ}$.
②连结$OC$,$OD$,如图,

$\because\angle ADC=\angle ACD=67.5^{\circ}$,$\therefore\angle CAD=180^{\circ}-2×67.5^{\circ}=45^{\circ}$,$\therefore\angle COD=90^{\circ}$,
$\because FC// AD$,$\therefore\angle AFC+\angle DAF=180^{\circ}$,$\therefore\angle DAF=\angle ADC$,$\overset\frown{AF}=\overset\frown{CD}$.
$\because CD$的长为$\frac{90\pi×2}{180}=\pi$,$\therefore\overset\frown{AF}$的长为$\pi$.
21. (8分)在平面直角坐标系中,设二次函数的表达式为 $ y = x^2 + (k + 1)x - (k + 2) $。
(1)若函数 $ y $ 的图象过点 $ (2, 0) $,求 $ k $ 的值;
(2)若函数 $ y $ 的图象的对称轴是 $ y $ 轴,求 $ k $ 的值;
(3)当 $ x < 2 $ 时,$ y $ 随 $ x $ 的增大而减小,当 $ x > 2 $ 时,$ y $ 随 $ x $ 的增大而增大,说明函数 $ y $ 的图象过点 $ (3, 0) $。
(1)若函数 $ y $ 的图象过点 $ (2, 0) $,求 $ k $ 的值;
(2)若函数 $ y $ 的图象的对称轴是 $ y $ 轴,求 $ k $ 的值;
(3)当 $ x < 2 $ 时,$ y $ 随 $ x $ 的增大而减小,当 $ x > 2 $ 时,$ y $ 随 $ x $ 的增大而增大,说明函数 $ y $ 的图象过点 $ (3, 0) $。
答案:
21.解:
(1)由题意,$\because$函数$y$的图象过点$(2,0)$,$\therefore4 + 2(k + 1)-(k + 2)=0$,$\therefore k=-4$.
(2)由题意,$\because$函数$y$的图象的对称轴是$y$轴,$\therefore-\frac{k + 1}{2}=0$,$\therefore k=-1$.
(3)由题意,$\because$当$x<2$时,$y$随$x$的增大而减小,当$x>2$时,$y$随$x$的增大而增大,$\therefore$抛物线的对称轴是直线$x = 2$,$\therefore-\frac{k + 1}{2}=2$,$\therefore k=-5$,$\therefore$抛物线的表达式为$y=x^{2}-4x + 3$,$\therefore$当$x = 3$时,$y=3^{2}-4×3 + 3 = 0$,$\therefore$函数$y$的图象过点$(3,0)$.
(1)由题意,$\because$函数$y$的图象过点$(2,0)$,$\therefore4 + 2(k + 1)-(k + 2)=0$,$\therefore k=-4$.
(2)由题意,$\because$函数$y$的图象的对称轴是$y$轴,$\therefore-\frac{k + 1}{2}=0$,$\therefore k=-1$.
(3)由题意,$\because$当$x<2$时,$y$随$x$的增大而减小,当$x>2$时,$y$随$x$的增大而增大,$\therefore$抛物线的对称轴是直线$x = 2$,$\therefore-\frac{k + 1}{2}=2$,$\therefore k=-5$,$\therefore$抛物线的表达式为$y=x^{2}-4x + 3$,$\therefore$当$x = 3$时,$y=3^{2}-4×3 + 3 = 0$,$\therefore$函数$y$的图象过点$(3,0)$.
查看更多完整答案,请扫码查看


