《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

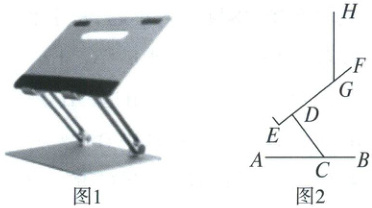
22. （10分）图1是某种笔记本电脑支架。如图2，其底座 $ AB $ 放置在水平桌面上，通过调节点 $ C $，$ D $ 处的角度，控制托盘 $ EF $ 的位置。电脑机身和屏幕分别用线段 $ EG $，$ GH $ 表示，$ CD = 16 cm $，$ EG = GH = 21 cm $，$ ED = 5 cm $。
（1）若 $ \angle ACD = 60° $，$ \angle CDG = 90° $。
① 为使屏幕与桌面保持垂直，求 $ \angle EGH $ 的度数；
② 求点 $ H $ 到桌面的最大距离（不计材料的厚度）。
（2）在（1）的情况下，保持 $ \angle CDG = 90° $，并逐渐减小 $ \angle ACD $ 的度数。圆圆同学说：“点 $ G $ 到桌面的距离越来越小。”点点同学说：“点 $ G $ 到桌面的距离先变大，后变小。”你认为谁的说法正确？请说明理由。

答案：
22.解：
(1)①如图1，延长$HG$交$AB$于点$M$，则$\angle BMG = 90^{\circ}$，

$\because\angle CDG=90^{\circ}$，$\therefore\angle CDE=90^{\circ}$.
$\because$四边形的外角和为$360^{\circ}$，$\angle ACD=60^{\circ}$，$\therefore\angle EGH=360^{\circ}-90^{\circ}-90^{\circ}-60^{\circ}=120^{\circ}$.
②如图2，作$DN\perp GM$于点$N$，$DH\perp AB$于点$P$，

$\therefore\angle DNG=90^{\circ}$，$\angle DPC=90^{\circ}$.
$\because\angle ACD=60^{\circ}$，$CD=16cm$，$\therefore DP=CD·\sin60^{\circ}=8\sqrt{3}(cm)$.
$\because EG=21cm$，$ED=5cm$，$\therefore DG=21 - 5 = 16(cm)$.
$\because\angle EGH=120^{\circ}$，$\therefore\angle DGN=60^{\circ}$，$\therefore GN=16×\cos60^{\circ}=8(cm)$，
$\because GH=21cm$，$\therefore$点$H$到桌面的最大距离为$21 + 8 + 8\sqrt{3}=(29 + 8\sqrt{3})cm$，答：点$H$到桌面的最大距离为$(29 + 8\sqrt{3})cm$.
(2)点点同学的说法正确.理由如下：设$\angle ACD=\alpha$，则$\angle DGH=180^{\circ}-\alpha$，$\therefore\angle DGN=\alpha$，$\therefore$点$G$到桌面的距离为$GN+DP=16×\cos\alpha+16×\sin\alpha$，
当$\angle ACD=60^{\circ}$时，点$G$到桌面的距离为$(8\sqrt{3}+8)cm$，当$\angle ACD=45^{\circ}$时，点$G$到桌面的距离为$16×\cos45^{\circ}+16×\sin45^{\circ}=16\sqrt{2}(cm)$，当$\angle ACD=30^{\circ}$时，点$G$到桌面的距离为$16×\cos30^{\circ}+16×\sin30^{\circ}=(8\sqrt{3}+8)cm$，
$\because8 + 8\sqrt{3}＜16\sqrt{2}$，$\therefore$点$G$到桌面的距离先变大，后变小，$\therefore$点点同学的说法正确.

23. （10分）在平面直角坐标系中，设函数 $ y_1 = (x - m)(x - n) $，$ y_2 = x^2 + mx + n $，其中 $ m \neq n $。
（1）若函数 $ y_1 $ 的图象过点 $ (0, 2) $，函数 $ y_2 $ 的图象过点 $ (1, 4) $，求 $ m^2 + n^2 $ 的值；
（2）若 $ 0 ＜ m ＜ n ＜ 4 $，判断函数 $ y_2 $ 与 $ x $ 轴的交点个数，说明理由；
（3）若函数 $ y_1 $ 和函数 $ y_2 $ 与 $ x $ 轴的交点均相同，求 $ m $，$ n $ 的值。

答案： 23.解：
(1)将$(0,2)$代入$y_{1}=(x - m)(x - n)$，将$(1,4)$代入$y_{2}=x^{2}+mx + n$，得$\begin{cases}mn=2\\1 + m + n = 4\end{cases}$，$\therefore m + n = 3$，$mn = 2$，$\therefore m^{2}+n^{2}=(m + n)^{2}-2mn=3^{2}-2×2=5$.
(2)$\because\Delta=m^{2}-4n$，$0＜m＜n＜4$，$\therefore\Delta＜0$，$\therefore$函数$y_{2}$与$x$轴无交点.
(3)$\because y_{1}=(x - m)(x - n)$，$\therefore$函数$y_{1}$与$x$轴的交点为$(m,0)$和$(n,0)$，$\therefore m + n=-m$，$mn = n$，$\therefore m = 0$，$n = 0$(舍去)或$m = 1$，$n=-2$.