《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

1. 已知二次函数 $ y = x^2 + x $，当 $ x = -1 $ 时，函数值是（ ）

A.-2
B.-1
C.0
D.1

答案： 1.C 解析：当$x=-1$时，$y=x^{2}+x=1-1=0$.故选：C.

2. 若 $ \frac{a}{2} = \frac{b}{3} $（$ a $，$ b $ 都不为 0），则（ ）

A.$ 2a = 3b $
B.$ 3a = 2b $
C.$ a + 2 = b + 3 $
D.$ a + 3 = b + 2 $

答案： 2.B 解析：$\because\frac{a}{2}=\frac{b}{3}$，$\therefore3a=2b$，$\therefore$只有选项B符合题意.故选：B.

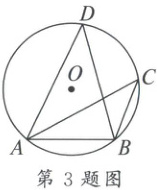
3. 如图，$ AB $ 是 $ \odot O $ 的弦，点 $ C $，$ D $ 都在 $ \odot O $ 上，若 $ \angle ACB = 40° $，则 $ \angle ADB = $（ ）

A.$ 20° $
B.$ 40° $
C.$ 50° $
D.$ 70° $

答案： 3.B 解析：由圆周角定理，得$\angle ADB=\angle ACB=40^{\circ}$.故选：B.

4. 下列事件中，属于随机事件的是（ ）

A.任意画一个三角形，其内角和是 $ 360° $
B.2张扑克牌，1张黑桃、1张红桃，从中随机抽取1张扑克牌是方块
C.掷一枚质地均匀的骰子，六个面上分别刻有1到6的点数，向上一面的点数大于0
D.拨打一个电话号码，电话正被占线中

答案： 4.D 解析：任意画一个三角形，其内角和是$360^{\circ}$，是不可能事件，则A不符合题意；2张扑克牌，1张黑桃、1张红桃，从中随机抽取1张扑克牌是方块，是不可能事件，则B不符合题意；掷一枚质地均匀的骰子，六个面上分别刻有1到6的点数，向上一面的点数大于0，是必然事件，故C不符合题意；拨打一个电话号码，电话正被占线中，是随机事件，则D符合题意.故选：D.

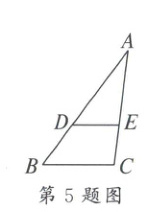
5. 如图，已知点 $ D $，$ E $ 分别在 $ \triangle ABC $ 的边 $ AB $，$ AC $ 上，$ DE // BC $。若 $ DE = 2k $，$ BC = 3k $，$ BD = 4 $，则 $ AD $ 的值为（ ）

A.2
B.4
C.6
D.8

答案： 5.D 解析：$\because DE// BC$，$DE=2k$，$BC=3k$，$\therefore\triangle ADE\backsim\triangle ABC$，$\therefore\frac{AD}{AB}=\frac{DE}{BC}=\frac{2k}{3k}=\frac{2}{3}$.
$\because BD=4$，$\therefore AB=AD+4$，$\therefore\frac{AD}{AD+4}=\frac{2}{3}$，$\therefore AD=8$.故选：D.

6. 一盒球（只有颜色不同）有15个红球、6个彩球（不是红色和白色）和1个白球，共22个球。设从中随机拿取1个球是红球的概率为 $ P $，则（ ）

A.$ 0 ＜ P ＜ \frac{1}{2} $
B.$ \frac{1}{2} ＜ P ＜ \frac{5}{7} $
C.$ \frac{5}{7} ＜ P ＜ \frac{3}{4} $
D.$ \frac{3}{4} ＜ P ＜ 1 $

答案： 6.B 解析：$\because$一盒球（只有颜色不同）有15个红球、6个彩球（不是红色和白色）和1个白球，共22个球，$\therefore$从中随机拿取1个球是红球的概率为$P=\frac{15}{22}$，$\because\frac{1}{2}＜\frac{15}{22}＜\frac{5}{7}$，$\therefore\frac{1}{2}＜P＜\frac{5}{7}$.故选：B.

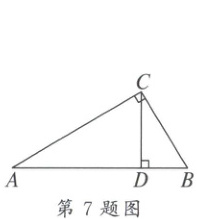
7. 如图，在 $ \triangle ABC $ 中，$ \angle ACB = 90° $，$ CD $ 是 $ AB $ 边上的高线，设 $ \angle A = \alpha $，则（ ）

A.$ BD = AB · \sin^2 \alpha $
B.$ BD = AB · \sin \alpha · \tan \alpha $
C.$ AD = AB · \cos \alpha · \sin \alpha $
D.$ AD = AB · \cos \alpha · \tan \alpha $

答案： 7.A 解析：由题知，$\because\angle ACB=90^{\circ}$，$CD$是$AB$边上的高线，$\therefore\angle A+\angle ACD=\angle ACD+\angle BCD=90^{\circ}$，$\therefore\angle A=\angle BCD$.
在不同的直角三角形中，根据正弦、余弦及正切的定义可知，$\sin\alpha=\frac{CD}{AC}=\frac{BC}{AB}=\frac{BD}{BC}$，$\cos\alpha=\frac{AD}{AC}=\frac{AC}{AB}=\frac{CD}{BC}$，$\tan\alpha=\frac{CD}{AD}=\frac{BC}{AC}=\frac{BD}{CD}$，$AB·\sin^{2}\alpha=AB·\frac{BC^{2}}{AB^{2}}=\frac{BC^{2}}{AB}$，由$\frac{BC}{AB}=\frac{BD}{BC}$，得$BC^{2}=AB· BD$，所以$\frac{BC^{2}}{AB}=\frac{AB· BD}{AB}=BD$，即$BD=AB·\sin^{2}\alpha$，故A选项符合题意；
$AB·\sin\alpha·\tan\alpha=AB·\frac{BC}{AB}·\frac{BC· BD}{CD· BC}=\frac{BC· BD}{CD}$，显然$BC$与$CD$一定不相等，所以$AB·\sin\alpha·\tan\alpha$一定不等于$BD$，故B选项不符合题意；
$AB·\cos\alpha·\sin\alpha=AB·\frac{AC}{AB}·\frac{CD}{AC}=CD$，显然$AD$与$CD$一定不相等，所以$AB·\cos\alpha·\sin\alpha$一定不等于$AD$，故C选项不符合题意；
$AB·\cos\alpha·\tan\alpha=AB·\frac{AC}{AB}·\frac{BC}{AC}=BC$，显然$AD$与$BC$不一定相等，所以$AB·\cos\alpha·\tan\alpha$不一定等于$AD$，故D选项不符合题意.故选：A.

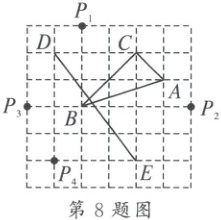
8. 如图，在 $ 6 × 6 $ 方格中，点 $ A $，$ B $，$ C $，$ D $，$ E $ 均在格点上，若 $ \triangle ABC $ 与 $ \triangle DEP_i (i = 1, 2, 3, 4) $ 相似，则符合条件的格点 $ P_i $ 是（ ）

A.点 $ P_1 $
B.点 $ P_2 $
C.点 $ P_3 $
D.点 $ P_4 $

答案：
8.C 解析：由题意，$\triangle ABC$是直角三角形，$BC=2AC$，

连结$DP_{3}$，$EP_{3}$，$\triangle DP_{3}E$是直角三角形，且$EP_{3}=2DP_{3}$，$\therefore\triangle ACB\backsim\triangle DP_{3}E$.故选：C.