第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
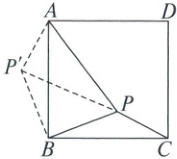
21. 如图,在正方形ABCD内有一点P,且PA=3,PB=2,PC=1。将线段BP绕点B逆时针旋转90°得到线段BP',连结AP',PP'。
(1)求证:△PBC≌△P'BA;
(2)求∠BPC的度数。
(1)求证:△PBC≌△P'BA;
(2)求∠BPC的度数。

答案:
21.
(1)证明:
∵在正方形ABCD内有一点P,PA=3,PB=
2,PC=1,线段BP绕点B逆时针旋转90°得到线段BP',
∴BP'=BP,BA=BC,∠P'BA=∠PBC,
∴△PBC≌△P'BA(SAS).
(2)解:
∵△PBC≌△P'BA,
∴P'A=PC=1,又$PP'=\sqrt{2}PB=2\sqrt{2}$
∴$P'A^{2}+P'P^{2}=1+8=3^{2}=PA^{2}$,
∴∠AP'P=90°,
∴∠BPC=∠AP'B=90°+45°=135°.
(1)证明:
∵在正方形ABCD内有一点P,PA=3,PB=
2,PC=1,线段BP绕点B逆时针旋转90°得到线段BP',
∴BP'=BP,BA=BC,∠P'BA=∠PBC,
∴△PBC≌△P'BA(SAS).
(2)解:
∵△PBC≌△P'BA,
∴P'A=PC=1,又$PP'=\sqrt{2}PB=2\sqrt{2}$
∴$P'A^{2}+P'P^{2}=1+8=3^{2}=PA^{2}$,
∴∠AP'P=90°,
∴∠BPC=∠AP'B=90°+45°=135°.
22. 关于x的一元二次方程$ax^{2} + \sqrt{2}cx + b = 0$,如果a,b,c满足$a^{2} + b^{2} = c^{2}$且a≠0,那么我们把这样的方程称为“勾系一元二次方程”。请解决下列问题:
(1)判断方程$x^{2} + 2x + 1 = 0$是不是“勾系一元二次方程”,并说明理由;
(2)求证:关于x的“勾系一元二次方程”$ax^{2} + \sqrt{2}cx + b = 0$必有实数根;
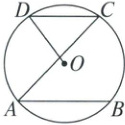
(3)如图,已知AB,CD是半径为8的⊙O的两条平行弦,AB=2a,CD=2b,且关于x的方程$ax^{2} + 8\sqrt{2}x + b = 0$是“勾系一元二次方程”,则∠BAC的度数为
(1)判断方程$x^{2} + 2x + 1 = 0$是不是“勾系一元二次方程”,并说明理由;
(2)求证:关于x的“勾系一元二次方程”$ax^{2} + \sqrt{2}cx + b = 0$必有实数根;
(3)如图,已知AB,CD是半径为8的⊙O的两条平行弦,AB=2a,CD=2b,且关于x的方程$ax^{2} + 8\sqrt{2}x + b = 0$是“勾系一元二次方程”,则∠BAC的度数为
45
°。
答案:
22.
(1)解:方程$x^{2}+2x+1=0$是“勾系一元二次方程”,理由如下:
$x^{2}+2x+1=0$,
由题意知:$a=1$,$b=1$,$c=\sqrt{2}$,
满足$1^{2}+1^{2}=(\sqrt{2})^{2}$且$1\neq0$,
故方程$x^{2}+2x+1=0$是“勾系一元二次方程”
(2)证明:
∵$ax^{2}+\sqrt{2}cx+b=0$是“勾系一元二次方程”,
∴$a^{2}+b^{2}=c^{2}$,
∵$(\sqrt{2}c)^{2}-4ab=2c^{2}-4ab=2a^{2}+2b^{2}-4ab=2(a-b)^{2}\geq0$,
∴$ax^{2}+\sqrt{2}cx+b=0$必有实数根.
(3)解:连结OC,OB,作OE⊥CD于E,EO的延长线交
AB于F.

∵关于$x$的方程$ax^{2}+8\sqrt{2}x+b=0$是“勾系一元二次方程”,
∴$a^{2}+b^{2}=8^{2}$,
∵AB//CD,OE⊥CD,
∴OF⊥AB,
∴∠OEC=∠OFB=90°,
∴$CE^{2}+OE^{2}=OC^{2}$,$OF^{2}+BF^{2}=OB^{2}$,$DE=EC=b$,$BF=AF=a$,
∵OC=OB=8,
∴$OE=\sqrt{OC^{2}-EC^{2}}=\sqrt{8^{2}-b^{2}}=a$,$OF=\sqrt{OB^{2}-BF^{2}}=\sqrt{8^{2}-a^{2}}=b$,
∴CE=OF,OE=BF,
∴△OEC≌△BFO(SSS),
∴∠EOC=∠OBF,
∵∠OBF+∠BOF=90°,
∴∠EOC+∠BOF=90°,
∴∠COB=90°,
∴∠BAC=$\frac{1}{2}$∠COB=45°.
故答案为45.
22.
(1)解:方程$x^{2}+2x+1=0$是“勾系一元二次方程”,理由如下:
$x^{2}+2x+1=0$,
由题意知:$a=1$,$b=1$,$c=\sqrt{2}$,
满足$1^{2}+1^{2}=(\sqrt{2})^{2}$且$1\neq0$,
故方程$x^{2}+2x+1=0$是“勾系一元二次方程”
(2)证明:
∵$ax^{2}+\sqrt{2}cx+b=0$是“勾系一元二次方程”,
∴$a^{2}+b^{2}=c^{2}$,
∵$(\sqrt{2}c)^{2}-4ab=2c^{2}-4ab=2a^{2}+2b^{2}-4ab=2(a-b)^{2}\geq0$,
∴$ax^{2}+\sqrt{2}cx+b=0$必有实数根.
(3)解:连结OC,OB,作OE⊥CD于E,EO的延长线交
AB于F.

∵关于$x$的方程$ax^{2}+8\sqrt{2}x+b=0$是“勾系一元二次方程”,
∴$a^{2}+b^{2}=8^{2}$,
∵AB//CD,OE⊥CD,
∴OF⊥AB,
∴∠OEC=∠OFB=90°,
∴$CE^{2}+OE^{2}=OC^{2}$,$OF^{2}+BF^{2}=OB^{2}$,$DE=EC=b$,$BF=AF=a$,
∵OC=OB=8,
∴$OE=\sqrt{OC^{2}-EC^{2}}=\sqrt{8^{2}-b^{2}}=a$,$OF=\sqrt{OB^{2}-BF^{2}}=\sqrt{8^{2}-a^{2}}=b$,
∴CE=OF,OE=BF,
∴△OEC≌△BFO(SSS),
∴∠EOC=∠OBF,
∵∠OBF+∠BOF=90°,
∴∠EOC+∠BOF=90°,
∴∠COB=90°,
∴∠BAC=$\frac{1}{2}$∠COB=45°.
故答案为45.
查看更多完整答案,请扫码查看


