《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

18. (8 分) 一个布袋里装有 3 个只有颜色不同的球，其中 2 个红球，1 个白球。
（1）求摸出一个球是红球的概率；
（2）第一次摸出 1 个球，记下颜色，放回摇匀，再摸出 1 个球，求两次都摸出红球的概率。（用树状图或列表来表示分析过程）

答案：
18.解：
(1)摸出一个球是红球的概率为$\frac{2}{3}$。
(2)画树状图如图，

共有9种等可能的结果，其中两个球都是红球的结果数为4，$\therefore$两次都摸出红球的概率为$\frac{4}{9}$。

19. (8 分) 如图，在边长为 1 的小正方形组成的网格中，$\triangle ABC$ 的三个顶点均在格点上。
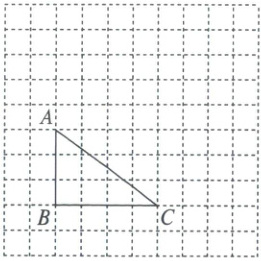
（1）将 $\triangle ABC$ 绕点 $C$ 顺时针旋转 $90^{\circ}$ 得 $\triangle A_1B_1C$，画出 $\triangle A_1B_1C$；
（2）在（1）的条件下，求点 $A$ 经过的路径长。（结果保留 $\pi$）

答案：
19.解：
(1)如图，$\triangle A_1B_1C$就是所求的三角形。
(2)$\because \angle ABC = 90°$，$AB = 3$，$BC = 4$，$\therefore AC = \sqrt{AB^2 + BC^2} = \sqrt{3^2 + 4^2} = 5$。$\because \triangle ABC$绕点C顺时针旋转$90°$得$\triangle A_1B_1C$，$\therefore A_1C = AC = 5$，$\angle ACA_1 = 90°$，$\therefore$点A经过的路径长为以C为圆心，半径长为5，且圆心角为$90°$的$\overset{\frown}{AA_1}$的长，$\because l_{\overset{\frown}{AA_1}} = \frac{90\pi × 5}{180} = \frac{5\pi}{2}$，$\therefore$点A经过的路径长为$\frac{5\pi}{2}$。