第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 二次函数 $ y = ( x - 3 ) ^ { 2 } + 2 $ 图象的顶点坐标是(
A.$ ( - 3, 2 ) $
B.$ ( 3, 2 ) $
C.$ ( - 3, - 2 ) $
D.$ ( 3, - 2 ) $
B
)A.$ ( - 3, 2 ) $
B.$ ( 3, 2 ) $
C.$ ( - 3, - 2 ) $
D.$ ( 3, - 2 ) $
答案:
1.B 解析:由题意,
∵二次函数为$y=(x - 3)^2+2$,
∴顶点为$(3,2)$.故选:B.
∵二次函数为$y=(x - 3)^2+2$,
∴顶点为$(3,2)$.故选:B.
2. 已知 $ \odot O $ 的半径为5,点 $ P $ 在 $ \odot O $ 外,则 $ OP $ 的长可能是(
A.3
B.4
C.5
D.6
D
)A.3
B.4
C.5
D.6
答案:
2.D 解析:
∵$\odot O$的半径为5,点$P$在$\odot O$外,
∴$OP>5$.故选:D.
∵$\odot O$的半径为5,点$P$在$\odot O$外,
∴$OP>5$.故选:D.
3. 下列事件,属于随机事件的是(
A.两个负数的和是正数
B.在一个只装有黑球的袋中摸出白球
C.任意画一个三角形,内角和为 $ 180 ^ { \circ } $
D.抛掷一枚硬币,正面朝上
D
)A.两个负数的和是正数
B.在一个只装有黑球的袋中摸出白球
C.任意画一个三角形,内角和为 $ 180 ^ { \circ } $
D.抛掷一枚硬币,正面朝上
答案:
3.D 解析:两个负数的和是正数是不可能事件,则A不符合题意;在一个只装有黑球的袋中摸出白球是不可能事件,则B不符合题意;任意画一个三角形,内角和为$180^{\circ}$是必然事件,则C不符合题意;抛掷一枚硬币,正面朝上是随机事件,则D符合题意.故选:D.
4. 已知 $ \frac { a } { b } = \frac { 3 } { 2 } $,则代数式 $ \frac { a - b } { b } $ 的值为(
A.$ \frac { 1 } { 2 } $
B.$ \frac { 1 } { 3 } $
C.$ \frac { 2 } { 5 } $
D.$ \frac { 3 } { 5 } $
A
)A.$ \frac { 1 } { 2 } $
B.$ \frac { 1 } { 3 } $
C.$ \frac { 2 } { 5 } $
D.$ \frac { 3 } { 5 } $
答案:
4.A 解析:
∵$\frac{a}{b}=\frac{3}{2}$,
∴$\frac{a - b}{b}=\frac{a}{b}-1=\frac{3}{2}-1=\frac{1}{2}$.故选:A.
∵$\frac{a}{b}=\frac{3}{2}$,
∴$\frac{a - b}{b}=\frac{a}{b}-1=\frac{3}{2}-1=\frac{1}{2}$.故选:A.
5. 如图,$ \triangle ABC $ 与 $ \triangle DEF $ 是位似图形,点 $ O $ 为位似中心,$ OA = AD $。若 $ \triangle ABC $ 的面积为4,则 $ \triangle DEF $ 的面积为(
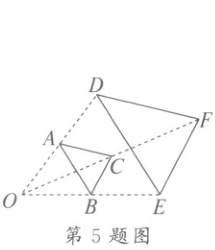
A.8
B.12
C.16
D.18
C
)
A.8
B.12
C.16
D.18
答案:
5.C 解析:
∵$\triangle ABC$与$\triangle DEF$是位似图形,
∴$\triangle ABC∽\triangle DEF$,$AB// DE$,
∴$\triangle OAB∽\triangle ODE$,
∵$OA = AD$,
∴$OA:OD = 1:2$,
∴$\frac{AB}{DE}=\frac{OA}{OD}=\frac{1}{2}$,
∴$\frac{S_{\triangle ABC}}{S_{\triangle DEF}}=(\frac{1}{2})^2=\frac{1}{4}$,
∵$\triangle ABC$的面积为4,
∴$\triangle DEF$的面积为16.故选:C.
∵$\triangle ABC$与$\triangle DEF$是位似图形,
∴$\triangle ABC∽\triangle DEF$,$AB// DE$,
∴$\triangle OAB∽\triangle ODE$,
∵$OA = AD$,
∴$OA:OD = 1:2$,
∴$\frac{AB}{DE}=\frac{OA}{OD}=\frac{1}{2}$,
∴$\frac{S_{\triangle ABC}}{S_{\triangle DEF}}=(\frac{1}{2})^2=\frac{1}{4}$,
∵$\triangle ABC$的面积为4,
∴$\triangle DEF$的面积为16.故选:C.
6. 小华同学根据学习二次函数的经验,用描点法画出了函数 $ y = \frac { 1 } { 9 } x ^ { 3 } - x $ 的图象。由图象可知,方程 $ \frac { 1 } { 9 } x ^ { 3 } - x = 1 $ 的实数根有(
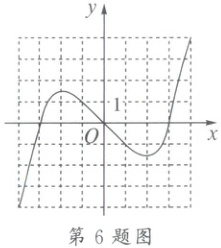
A.1个
B.2个
C.3个
D.4个
C
)
A.1个
B.2个
C.3个
D.4个
答案:
6.C 解析:观察函数$y=\frac{1}{9}x^3 - x$的图象可知,图象与直线$y = 1$有3个交点,
∴方程$\frac{1}{9}x^3 - x = 1$的实数根有3个.故选:C.
∴方程$\frac{1}{9}x^3 - x = 1$的实数根有3个.故选:C.
7. 沈括在《梦溪笔谈》中收录了计算圆弧长度的“会圆术”,主要思路是局部以直代曲,进行近似计算。如图,$ \overset{\frown}{AB} $ 是以 $ O $ 为圆心、$ OA $ 长为半径的圆弧,$ C $ 是弦 $ AB $ 的中点,$ D $ 是 $ \overset{\frown}{AB} $ 的中点,则 $ \overset{\frown}{AB} $ 长度的近似值 $ l = AB + \frac { C D ^ { 2 } } { O A } $。若 $ C D = 2 $,$ AB = 8 $,则 $ l = $(
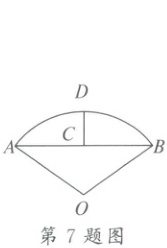
A.8.8
B.8.7
C.8.6
D.8.5
A
)
A.8.8
B.8.7
C.8.6
D.8.5
答案:
7.A 解析:如图,连结$OC$.设$OA = r$.

∵$C$是弦$AB$的中点,$D$是$\overset{\frown}{AB}$的中点,
∴$O$,$C$,$D$共线,$OD\perp AB$,
∴$AC = CB=\frac{1}{2}AB = 4$,在$Rt\triangle AOC$中,$OA^2=AC^2 + OC^2$,
∴$r^2=4^2+(r - 2)^2$,
∴$r = 5$,
∴$OA = 5$,
∴$AB$长度的近似值$l=AB+\frac{CD^2}{OA}=8+\frac{2^2}{5}=8.8$.故选:A.
7.A 解析:如图,连结$OC$.设$OA = r$.

∵$C$是弦$AB$的中点,$D$是$\overset{\frown}{AB}$的中点,
∴$O$,$C$,$D$共线,$OD\perp AB$,
∴$AC = CB=\frac{1}{2}AB = 4$,在$Rt\triangle AOC$中,$OA^2=AC^2 + OC^2$,
∴$r^2=4^2+(r - 2)^2$,
∴$r = 5$,
∴$OA = 5$,
∴$AB$长度的近似值$l=AB+\frac{CD^2}{OA}=8+\frac{2^2}{5}=8.8$.故选:A.
查看更多完整答案,请扫码查看


