《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

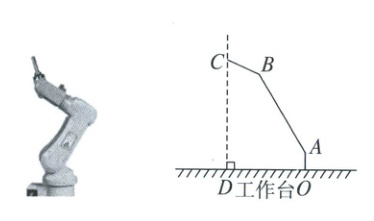
14. 2022年6月5日，“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图，OA是垂直于工作台的移动基座，AB，BC为机械臂，$OA = 1m$，$AB = 5m$，$BC = 2m$，$\angle ABC = 143^{\circ}$.机械臂端点C到工作台的距离$CD = 6m$.
(1)求A，C两点之间的距离；
(2)求OD长.(结果精确到0.1m，参考数据：$\sin37^{\circ}\approx0.60$，$\cos37^{\circ}\approx0.80$，$\tan37^{\circ}\approx0.75$，$\sqrt{5}\approx2.24$)

答案：
14. 解:

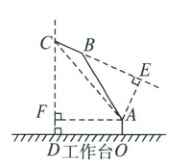
(1) 如图,过点 $ A $ 作 $ AE \perp CB $,垂足为 $ E $,连结 $ AC $,
在 $ Rt \triangle ABE $ 中,$ AB = 5\ m $,$ \angle ABE = 37^{\circ} $,
$\because \sin \angle ABE=\frac{AE}{AB},\cos \angle ABE=\frac{BE}{AB}$,
$\therefore \frac{AE}{5} \approx 0.60,\frac{BE}{5} \approx 0.80$,
$\therefore AE = 3\ m,BE = 4\ m$,
$\therefore CE = 6\ m$,
在 $ Rt \triangle ACE $ 中,由勾股定理,得 $ AC=\sqrt{3^{2}+6^{2}} = 3\sqrt{5}\approx 6.7\ m $.
(2) 过点 $ A $ 作 $ AF \perp CD $,垂足为 $ F $,
$\therefore FD = AO = 1\ m$,
$\therefore CF = 5\ m$,
在 $ Rt \triangle ACF $ 中,由勾股定理,得 $ AF=\sqrt{45 - 25}=2\sqrt{5}\ m $.
$\therefore OD = 2\sqrt{5}\ m \approx 4.5\ m $.