《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

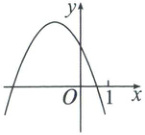
9. 已知二次函数$y=ax^{2}+2ax+c(a\neq0)$的图象如图所示，则下列说法：①$ac＞0$；②若点$P(-2,m)$，$Q(0.5,n)$都在该抛物线上，则$m＜n$；③$3a+c＞0$；④方程$ax^{2}+(2a+1)x+c=0$有两个不相等的实数根。正确的有(A)

A.1个
B.2个
C.3个
D.4个

答案：
9.A　解析:
∵抛物线开口向下，
∴a＜0,
∵抛物线与y轴的交点在y轴正半轴，
∴c＞0,
∴ac＜0,
　　故①错误;
　　抛物线的对称轴为直线x=−$\frac{2a}{2a}$=−1,抛物线开口向下，
∵−1−(−2)=1＜0.5−(−1)=1.5,
∴m＞n,
　　故②错误;
　　由图象知，当x=1时,y＜0，
　　即a+2a+c=3a+c＜0,
　　故③错误;
　　如图所示:
　　　　　　　　　　　　　　　　
∵二次函数y=ax²+2ax+c(a≠0)的图象与直线y=−x有两个交点,
∴方程ax²+(2a+1)x+c=0有两个不相等的实数根，
　　故④正确.
　　综上，正确的个数有1个.
　　故选A.

10. 定义：若一次函数的图象与二次函数的图象有两个交点，并且都在坐标轴上，则称二次函数为一次函数的轴点函数。函数$y=-x+c$($c$为常数，$c＜0$)的图象与$x$轴交于点$M$，其轴点函数$y=ax^{2}+bx+c$与$x$轴的另一交点为$N$。若$ON=\frac{1}{4}OM$，则$b$的值为(D)

A.$-5$
B.$3$或$-1$
C.$3$
D.$-5$或$3$

答案： 10.D　解析:
∵函数y=−x+c(c为常数,c＜0)的图象与x轴交于点M,
∴M(c,0).
∴OM=−c.
∵ON=$\frac{1}{4}$OM,
∴ON=−$\frac{1}{4}$c,
∴N(±$\frac{1}{4}$c,0).
∵其轴点函数y=ax²+bx+c与x轴的两个交点为M,N,
∴$\begin{cases}ac^{2}+bc + c = 0\\a·(\frac{1}{4}c)^{2}+b·(\frac{1}{4}c)+c = 0\end{cases}$或$\begin{cases}ac^{2}+bc + c = 0\\a·(-\frac{1}{4}c)^{2}+b·(-\frac{1}{4}c)+c = 0\end{cases}$
∴b=−5或b=3.
　　故选D.

11. 请写出一个开口向下，经过原点的二次函数的表达式y=-x²。

答案： 11.y=-x²(答案不唯一)　解析:开口向下，经过原点的二次函数的表达式可以是y=−x²(答案不唯一).

12. 已知二次函数$y=x^{2}+2x+c$的图象与坐标轴恰有两个交点，则$c=$0或1。

答案： 12.0或1　解析:
∵二次函数y=x²+2x+c的图象与坐标轴恰有两个交点，
　　①若c=0时,函数y=x²+2x与x轴有两点交点(0,0),(−2,0),符合题意.
　　②当c≠0时,当x=0时,y=c,即图象与y轴交于点(0,c),
∴二次函数y=x²+2x+c的图象与x轴必有一个交点.
∴b²−4ac=2²−4c=0.
∴c=1.
　　综上,c=0或1.

13. 已知$y=2x-8$，$S=xy$，当$-1\leq x\leq3$时，则$S$的最大值为10。

答案： 13.10　解析:
∵y=2x−8,
∴S=xy=2x²−8x=2(x−2)²−8,
∵−1≤x≤3,
∴当x=−1时,S的最大值为2×(−1−2)²−8=10.

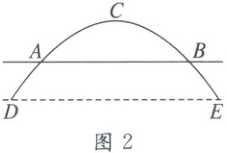
14. 如图1是一座抛物线形拱桥，图2是其示意图，桥拱与水平桥面相交于$A$，$B$两点，桥拱最高点$C$到$AB$的距离为$9m$，$AB=36m$，$D$，$E$为桥拱底部的两点，且$DE// AB$，点$E$到直线$AB$的距离为$7m$，则$DE$的长为48m。

答案：
14.48　解析:如图所示，建立平面直角坐标系
　　　　　　　
　设AB与y轴交于点H，
∵AB=36,
∴AH=BH=18,
　由题可知:
　OH=7,CH=9,
∴OC=9+7=16.
　设该抛物线的表达式为y=ax²+k，
∵顶点C(0,16),
∴抛物线y=ax²+16,
代入点(18,7)
∴7=18×18a+16,
∴7=324a+16,
∴324a=−9,
∴a=−$\frac{1}{36}$,
∴抛物线y=−$\frac{1}{36}$x²+16,
　　当y=0时,0=−$\frac{1}{36}$x²+16,
∴$\frac{1}{36}$x²=16,
∴x²=16×36,
∴x=±24,
∴E(24,0),D(−24,0),
∴OE=OD=24,
∴DE=OD+OE=24+24=48(m).

15. 点$M(x_{1},y_{1})$，$N(x_{2},y_{2})$在二次函数$y=x^{2}-2x+1$的图象上，若$m-1＜x_{1}＜m$，$m+1＜x_{2}＜m+2$时，都有$y_{1}\neq y_{2}$，则$m$的取值范围是m≥1或m≤0。

答案： 15.m≥1或m≤0　解析:二次函数y=x²−2x+1的对称轴为直线x=−$\frac{b}{2a}$=1,
∵m−1＜x₁＜m,m+1＜x₂＜m+2时,都有y₁≠y₂,
　x=$\frac{x₁+x₂}{2}$表示x₁与x₂表示的点连线的中垂线，根据题意则有m＜$\frac{x₁+x₂}{2}$＜m+1,
∴要使y₁≠y₂,则对称轴不在$\frac{x₁+x₂}{2}$可取范围内，
　　即m≥1或m+1≤1,
　解得m≥1或m≤0.

16. 图1是一个瓷碗，图2是其截面图，碗体$DEC$呈抛物线状(碗体厚度不计)，碗口宽$CD=12cm$，此时面汤最大深度$EG=8cm$。
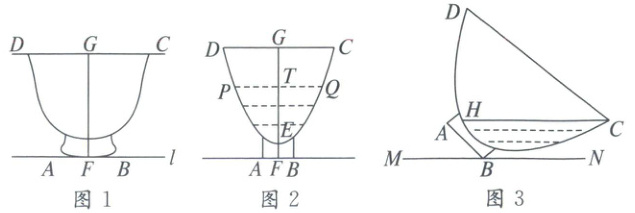
(1)当面汤的深度$ET$为$4cm$时，汤面的直径$PQ$长为6$\sqrt{2}$cm；
(2)如图3，把瓷碗绕点$B$缓缓倾斜倒出部分面汤，当$\angle ABM=45^{\circ}$时停止，此时碗中液面宽度$CH=$$\frac{15\sqrt{2}}{2}$cm。

答案：
16.
(1)6$\sqrt{2}$　
(2)$\frac{15\sqrt{2}}{2}$　解析:
(1)以F为原点，直线AB为x轴，直线EF为y轴，建立平面直角坐标系，如图:
　　　　　　　　　
　设点E的坐标为(0,c),则抛物线的表达式为y=ax² +c,
　则点C(6,8+c),点Q(x_Q,4+c),
　将点C,Q的坐标分别代入抛物线表达式，得
　　$\begin{cases}8 + c = 36a + c\\4 + c = ax_{Q}^{2}+ c\end{cases}$，解得$\begin{cases}a = \frac{2}{9}\\x_{Q}= 3\sqrt{2}\end{cases}$
　即抛物线的表达式为y=$\frac{2}{9}$x²+c,①
PQ=2x_Q=6$\sqrt{2}$
(2)将瓷碗绕点B缓缓倾斜倒出部分面汤，当∠ABM=45°时停止，所以旋转前CH与水平方向的夹角为45°，设直线CH的表达式为y=x+b,
　将点C的坐标代入上式，得b=2+c，故直线CH的表达式为y=x+2+c,②
　联立①②并整理得2x²−9x−18=0,
　则x₁+x₂=$\frac{9}{2}$,x₁x₂=−9,
　则(x₁−x₂)²=(x₁+x₂)²−4x₁x₂=$\frac{225}{4}$,
　则|x₁−x₂｜=$\frac{15}{2}$,
　由CH的表达式可知，其与x轴的夹角为45°，
　则CH=$\sqrt{2}$|x₁−x₂|=$\frac{15\sqrt{2}}{2}$.