《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

9. 黄金矩形的宽、长之比为黄金分割率，换言之，矩形的短边长与长边长的比为$\frac{\sqrt{5} - 1}{2}$，黄金分割率和黄金矩形能够给画面带来美感，令人愉悦。在很多艺术品以及大自然中都能找到它，希腊雅典的巴特农神庙就是一个很好的例子。若一个黄金矩形的长边的长为$8$，则短边长$m$的值最接近的是(B)

A.$4$
B.$5$
C.$6$
D.$7$

答案： 9.B　解析:8×$\frac{\sqrt{5}−1}{2}$≈8×0.618=4.944≈5。
　故选B。

10. 如图，正方形$ABCD$的边长为$4$，点$E$，$F$分别在边$DC$，$BC$上，且$BF = CE$，$AE$平分$\angle CAD$，连结$DF$，分别交$AE$，$AC$于点$G$，$M$，$P$是线段$AG$上的一个动点，过点$P$作$PN \perp AC$，垂足为$N$，连结$PM$。有下列四个结论：①$AE$垂直平分$DM$；②$PM + PN$的最小值为$3\sqrt{2}$；③$CF^2 = GE · AE$；④$S_{\triangle ADM} = 4\sqrt{2}$。其中正确的是(D)

A.①②
B.②③④
C.①③
D.①③④

答案：
10.D　解析:①
∵四边形ABCD是正方形，
∴AD=DC=BC，∠ADC=∠DCB=90°，
∵BF=CE，
∴BC−BF=DC−CE，
　　即CF=DE。
　在△ADE和△DCF中，
$\begin{cases} AD=DC \\ \angle ADE=\angle DCF \\ DE=CF \end{cases}$
∴△ADE≌△DCF(SAS)，
∴∠DAE=∠CDF。
∵∠CDF+∠ADG=90°，
∴∠DAE+∠ADG=90°，
∴∠AGD=90°，
∴∠AGM=90°，
∴∠AGM=∠AGD。
∵AE平分∠CAD，
∴∠MAG=∠DAG。
　又AG为公共边，
∴△AGM≌△AGD(ASA)，
∴GM=GD。
　又
∵∠AGM=∠AGD=90°，
∴AE垂直平分DM。
　故①正确。
　②如图，连结BD与AC交于点O，交AG于点H，连结HM。

∵四边形ABCD是正方形，
∴AC⊥BD，
　　即DO⊥AM。
∵AE垂直平分DM，
∴HM=HD，
　　当点P与点H重合时，PM+PN的值最小，此时PM +PN=HM+HO=HD+HO=DO，即PM+PN的最小值是DO的长。
∵正方形ABCD的边长为4，
∴AC=BD=4$\sqrt{2}$，
∴DO=$\frac{1}{2}$BD=2$\sqrt{2}$，
　　即PM+PN的最小值为$2\sqrt{2}$。
　　故②错误。
　　③
∵AE垂直平分DM，
∴∠DGE=90°，
∵∠ADC=90°，
∴∠DGE=∠ADE，
　　又
∵∠DEG=∠AED，
∴△DGE∽△ADE，
∴$\frac{DE}{AE}$=$\frac{GE}{DE}$，
　　即$DE^2=GE · AE$。
　　由①知CF=DE，
∴$CF^2=GE · AE$。
　　故③正确。
　　④
∵AE垂直平分DM，
∴AM=AD=4，
　　又DO=2$\sqrt{2}$，
∴$S_{\triangle ADM}=\frac{1}{2}AM · DO=\frac{1}{2} × 4 × 2\sqrt{2}=4\sqrt{2}$。
　　故④正确。
　　综上，正确的是①③④。
　　故选D。

11. 已知线段$a$，$b$，$c$，其中$c$是$a$，$b$的比例中项，若$a = 9\ cm$，$b = 4\ cm$，则线段$c =$6$cm$。

答案： 11.6　解析:根据比例中项的概念结合比例的基本性质，得比例中项的平方等于两条线段的乘积。
∵c是a、b的比例中项，
∴$c^2=4 × 9$，
　　解得c=±6，(线段是正数，负值舍去)，
　　则线段c=6cm。

12. 如图，以点$O$为位似中心，将五边形$ABCDE$放大后得到五边形$A'B'C'D'E'$，已知$OA = 10\ cm$，$OA' = 20\ cm$，则五边形$ABCDE$的周长与五边形$A'B'C'D'E'$的周长比是1:2。

答案： 12.1:2　解析:
∵以点O为位似中心，将五边形ABCDE放大后得到五边形A'B'C'D'E'，OA=10cm，OA'=20cm，
∴五边形ABCDE与五边形A'B'C'D'E'的位似比为10:20=1:2，
∴五边形ABCDE的周长与五边形A'B'C'D'E'的周长比是1:2。

13. 如图，在$\triangle ABC$中，点$D$，$E$分别在边$AB$，$AC$上，若$DE // BC$，$\frac{AD}{DB}=\frac{2}{3}$，$DE = 6\ cm$，则$BC$的长为15$cm$。

答案： 13.15　解析:
∵DE//BC，
∴△ADE∽△ABC，
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$。
∵$\frac{AD}{DB}$=$\frac{2}{3}$，
∴$\frac{AD}{AB}$=$\frac{2}{5}$，
∴$\frac{DE}{BC}$=$\frac{2}{5}$。
∵DE=6cm，
∴BC=15cm。

14. 如图，$\triangle ABC$中，边$BC = 12\ cm$，高$AD = 6\ cm$，边长为$x$的正方形$PQMN$的一边在$BC$上，其余两个顶点分别在$AB$，$AC$上，则正方形的边长$x =$4$cm$。

答案：
14.4　解析:如图，
　　　　　　　　　
∵PN//BC，
∴△APN∽△ABC，
∴$\frac{PN}{BC}$=$\frac{AI}{AD}$，即$\frac{x}{12}$=$\frac{6−x}{6}$，
　　解得x=4cm。

15. 如图，平面直角坐标系中，已知点$A(8,0)$和点$B(0,6)$，点$C$是$AB$的中点，点$P$在折线$AOB$上，直线$CP$截$\triangle AOB$所得的三角形与$\triangle AOB$相似，那么点$P$的坐标是______。

答案：
15.(0,3)，(4,0)，($\frac{7}{4}$,0)　　解析:当PC//OA时，△BPC ∽△BOA，
　　由点C是AB的中点，可得P为OB的中点，
　　此时点P的坐标为(0,3)；
　　当PC//OB时，△ACP∽△ABO，
　　由点C是AB的中点，可得P为OA的中点，
　　此时点P的坐标为(4,0)；
　　当PC⊥AB时，如图，
　　　　　　　　　　
∵∠CAP=∠OAB，
∴Rt△APC∽Rt△ABO，
∴$\frac{AC}{OA}$=$\frac{AP}{AB}$，
∵点A(8,0)和点B(0,6)，
∴AB=$\sqrt{6^2+8^2}$=10，
∵点C是AB的中点，
∴AC=5，
∴$\frac{5}{8}$=$\frac{AP}{10}$，
∴AP=$\frac{25}{4}$，
∴OP=OA−AP=8−$\frac{25}{4}$=$\frac{7}{4}$，
　此时点P的坐标为($\frac{7}{4}$,0)。
　　综上所述，满足条件的点P的坐标为(0，3)，(4，0)，($\frac{7}{4}$,0)。

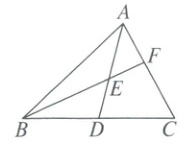
16. 如图，已知$D$是$BC$的中点，$E$是$AD$的中点，则$AF:FC =$1:2。

答案：
16.1:2　解析:如图，过点D作DM//AC，交BF于M，则△BDM∽△BCF，△DEM∽△AEF。
　　由△BDM∽△BCF，D是BC的中点，可知，$\frac{DM}{FC}$=$\frac{BD}{BC}$=$\frac{1}{2}$，
　　则FC=2DM。
　　由△DEM∽△AEF，E是AD的中点，得AF=DM，因而AF:FC=DM:2DM=1:2。
　　　　　　　　　　

17. 已知线段$a$，$b$，$c$满足$\frac{a}{3}=\frac{b}{2}=\frac{c}{6}$，且$a + 2b + c = 26$。
（1）求$a$，$b$，$c$的值；
（2）若线段$x$是线段$a$，$b$的比例中项，求$x$。

答案： 17.解:
(1)设$\frac{a}{3}$=$\frac{b}{2}$=$\frac{c}{6}$=k，
　　则a=3k，b=2k，c=6k，
∴3k+2×2k+6k=26，
　　解得k=2，
∴a=3×2=6，
　　b=2×2=4，
　　c=6×2=12。
(2)
∵线段x是线段a、b的比例中项，
∴$x^2=ab=6 × 4=24$，
∴$x=2\sqrt{6}$。