《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

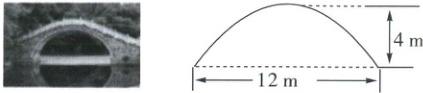
21. （6分）如图为一座拱桥的示意图，桥洞的拱形是抛物线，已知水面宽12m，桥洞顶部离水面4m。
（1）请在示意图中建立合适的平面直角坐标系，并求出抛物线的函数表达式；
（2）若有一艘船的宽度为4m，高度为3m，则这艘船能否从该桥下通过？

答案：
21.解:
(1)答案不唯一.如图，由题意，以水面中心为坐标原点建立平面直角坐标系，
　　　　　　　　
∴$A(-6,0)$，$B(6,0)$，顶点$C(0,4)$.设$y = ax^2 + 4$，把$B(6,0)$代入上式，
∴$36a + 4 = 0$，
∴$a=-\frac{1}{9}$，
∴$y=-\frac{1}{9}x^2 + 4$.
(2)由题意，
∵船的宽度为4m，
∴令$x = 2$，则$y=-\frac{1}{9}×2^2 + 4=\frac{32}{9}=3\frac{5}{9}＞3$，
∴这艘船能从该桥下通过.

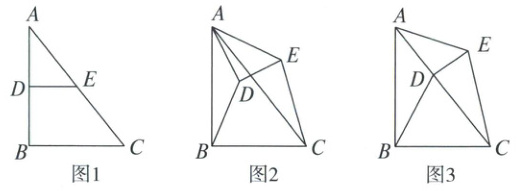
22. （6分）如图1，在 $ \triangle ABC $ 中，$ \angle A B C = 90 ^ { \circ } $，$ A B = 8 $，$ B C = 6 $，分别取 $ AB $，$ AC $ 的中点 $ D $，$ E $，连结 $ DE $。如图2，将图1中的 $ \triangle ADE $ 绕点 $ A $ 逆时针旋转，连结 $ BD $，$ CE $。
（1）在旋转过程中，$ CE $ 与 $ BD $ 之间存在怎样的数量关系？
（2）当点 $ D $ 落在边 $ AC $ 上时（如图3），求 $ BD $ 的长。

答案： 22.解:
(1)$CE=\frac{5}{4}BD$.如题图1，
∵$\angle ABC = 90^{\circ}$，$AB = 8$，$BC = 6$，
∴$AC=\sqrt{AB^2 + BC^2}=\sqrt{8^2 + 6^2}=10$，
∵$D$，$E$分别是$AB$，$AC$的中点，
∴$AD = BD=\frac{1}{2}AB = 4$，$AE = CE=\frac{1}{2}AB = 5$，如题图2，由旋转得$\angle CAE=\angle BAD$，
∴$\frac{AE}{AD}=\frac{AC}{AB}=\frac{10}{8}=\frac{5}{4}$，
∵$\frac{AE}{AD}=\frac{AC}{AB}$，
∴$\triangle CAE∽\triangle BAD$，
∴$\frac{CE}{BD}=\frac{AE}{AD}=\frac{5}{4}$，
∴$CE=\frac{5}{4}BD$.
(2)如题图1，
∵$D$，$E$分别是$AB$，$AC$的中点，$BC = 6$，
∴$DE// BC$，$DE=\frac{1}{2}BC = 3$，
∴$\angle ADE=\angle ABC = 90^{\circ}$，如题图3，
∵点$D$在$AC$上，$\angle ADE = 90^{\circ}$，
∴$\angle CDE = 90^{\circ}$，
∵$AC = 10$，$AD = 4$，$DE = 3$，
∴$CD = AC - AD = 10 - 4 = 6$，
∴$CE=\sqrt{CD^2 + DE^2}=\sqrt{6^2 + 3^2}=3\sqrt{5}$，
∵$CE=\frac{5}{4}BD$，
∴$\frac{5}{4}BD=3\sqrt{5}$，
∴$BD=\frac{12\sqrt{5}}{5}$，
∴$BD$的长是$\frac{12\sqrt{5}}{5}$.